城市路(Dijkstra)

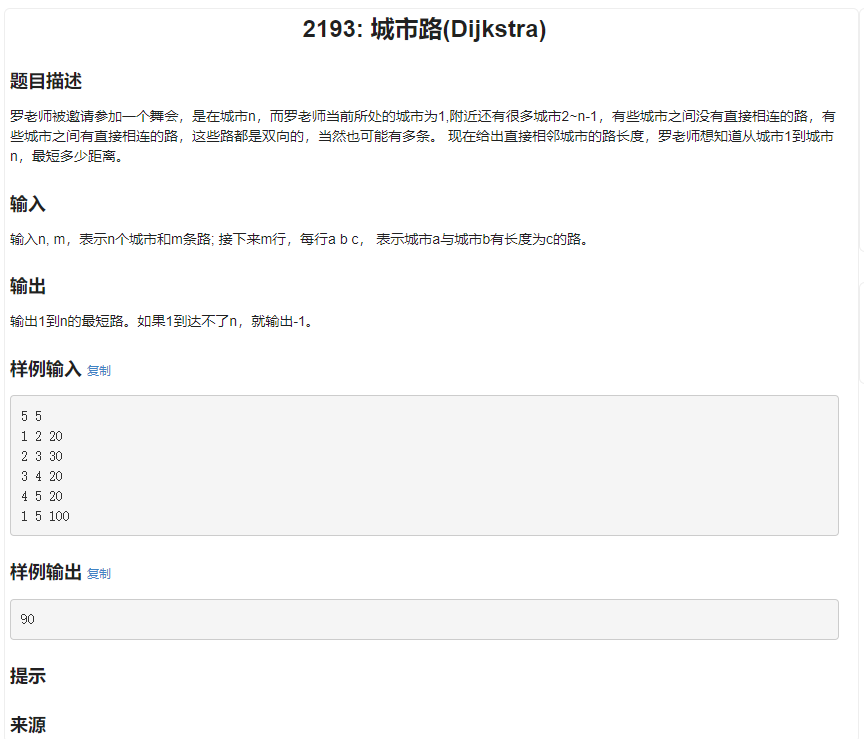
这道题目需要用到

Dijkstra plus 版（堆优化）

模板还是一样就是有几个点值得注意

1.这里用的是优先队列，原版需要搜出最小，并且没用过的点，省时间就剩在这里用小根堆就可以完美解决这个问题。

2.模拟链表（我认为有亿 一点难度）需要h,e,w,ne来模拟。

3.还有一个add（a,b,c）函数，表示在链表中加入从a到b距离为c。

void add(int a, int b, int c)  // 添加一条边a->b，边权为c
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

4.更行的思路（有改动） 我们在i不为最后一个值的情况下来判断是走A线路（长度为dist[j]）好还是B线路好（长度为distance+w[i]）.

5.小细节，在输入时因为是无向图所以要加两次像

　　　　　　　　

    add(x, y, z);
    add(y, x, z); 

程序：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 150010;
typedef pair<int,int> PII;
int h[N],e[N],w[N],ne[N],n,m,dist[N],idx;
bool st[N];
void add(int a, int b, int c)  // 添加一条边a->b，边权为c
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int d()
{
    dist[1]=0;
    priority_queue<PII,vector<PII>,greater<PII>> heap;
    heap.push({0,1});
    while(heap.size())
    {
        auto t=heap.top();
        heap.pop();
        int ver=t.second,distance=t.first;
        if(st[ver]) continue;
        st[ver]=1;
        for(int i=h[ver];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(dist[j]>distance+w[i])
            {
                dist[j]=distance+w[i];
                heap.push({dist[j],j});
            }
        }
    }
    if(dist[n]==0x3f3f3f3f) return -1;
    else return dist[n];
}
int main()
{
    scanf("%d%d", &n, &m);
    memset(dist,0x3f,sizeof dist);
    memset(h,-1,sizeof h);
    while (m -- )
    {
        int x,y,z;
        scanf("%d%d%d", &x, &y,&z);
        add(x, y, z);
        add(y, x, z);
    }
    cout<<d()<<endl;
    return 0;
}