在许多生产时间问题中，我们根据已知条件往往会列出一个一元非线性方程，一个最典型的例子就是银行存款的问题，由于其利息需要基于前一年的本息和，因此列出来的方程x的指数往往是高次的。还有物理问题当中一系列用微分方程导出的一元非线性方程。因此如何求解一元非线性方程，是计算数学要解决的重要问题之一。

牛顿法：

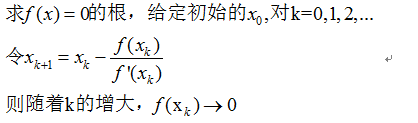
牛顿法可以通过Taylor定理导出：

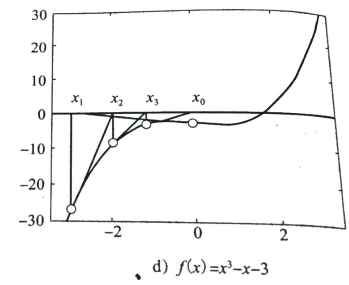
不幸的是，单纯的牛顿法并不是使用所有情况的，下面给出一个经过较为精确的绘图利用牛顿迭代最终无解的情况：

《Numerical Methods》-chaper4-一元非线性方程的解的更多相关文章

  1. Numerical Methods with MATLAB（1）

    目前正在阅读MATLAB相关的书籍:Numerical Methods with MATLAB,现在感觉这本书写的还行, 细致基础,而且写的比较清楚,同时把malab和数值算法结合在一起. 目前刚看完 ...

  2. Python编写“求一元二次方程的解”

    #求一元二次方程的解 import math def equation(a,b,c): h=b*b-4*a*c #一元二次方程的解,百度来的 if h>=0: x1=(-b+math.sqrt( ...

  3. 《Numerical Methods》-chaper7-解线性方程组的直接方法和最小二乘问题

    基于我们在线性代数中学习过的知识,我们知道解线性方程组本质上就是Gauss消元,也就是基于增广矩阵A的矩阵初等变换.关于数学层面的内容这里不做过多的介绍,这里的侧重点是从数值计算的角度来看这些常见的问 ...

  4. Java一元操作符++详解

    废话不多说,直接上代码. package com.coshaho.learn; /** * * OperatorLearn.java Create on 2016-11-13 下午8:38:15 * ...

  5. Numerical methods in enginering with python3 (1)

    <> (1) Numpy 库 Numpy中的矩阵函数 np.diagonal(A) 返回由A中的主对角元素组成的一维矩阵 np.diagonal(A,1) 返回由A中的第一副对角元素组成的 ...

  6. 一元二次方程解法的实现（Python）

    请定义一个函数quadratic(a, b, c),接收3个参数,返回一元二次方程: ax2 + bx + c = 0的两个解. 提示:计算平方根可以调用math.sqrt()函数   # -*- c ...

  7. C语言碰到的一元二次方程

    最近开始在学习C语言,看视频,是http://www.rjzxw.com/jc-74-1.html 碰到老师讲的一元二次方程例子,不懂,所以找了下资料,看了网上一元二次方程的视频(是自己太浮躁了,听不 ...

  8. Understanding about numerical stability, convergence and consistency

    In a computer simulation of the real world, physical quantities, which usually have continuous distr ...

  9. P与NP问题详解

    P,NP,NPC问题,这或许是众多OIer最大的误区之一. 本文就为大家详细讲解如上三个问题. 前序: 你会经常看到网上出现“这怎么做,这不是NP问题吗”.“这个只有搜了,这已经被证明是NP问题了”之 ...

随机推荐

  1. delphi 编写一个dos 窗体

    + //dos 仿真程序 delphi 窗体实现!   function GetDosOutput(CommandLine: string; Work: string = 'C:\'): string ...

  2. js获取当前url参数

    //抓取url参数 function GetRequest() { var url = location.search; //获取url中"?"符后的字串 var theReque ...

  3. Tuning “enq:TX – row lock contention” events

    enq是一种保护共享资源的锁定机制,一个排队机制 排它机制从一个事务的第一次改变直到rollback or commit 结束这个事务, TX等待mode是6,当一个session 在一个表的行级锁定 ...

  4. 利用SQL进行推理

    数据库环境:SQL SERVER 2008R2 有如下需求: Baker, Cooper, Fletcher, Miller and Smith住在一座房子的不同楼层.Baker 不住顶层.Coope ...

  5. Objective c 自动释放池

    学IOS 的大家都知道,IOS 一共有三种内存管理方式:MRC .ARC.自动释放池.我按照我个人的理解简述一下自动释放池,希望能给大家一点帮助,如有错误请大家及时批评指正. 自动释放池有几个特点:1 ...

  6. localStorage.ie6.js

    !window.localStorage && function() { window.localStorage = {}; var prefix = 'data-userdata' ...

  7. [设计模式]解释器(Interpreter)之大胆向MM示爱吧

    为方便读者,本文已添加至索引: 设计模式 学习笔记索引 写在前面 “我刚写了个小程序,需要你来参与下.”我把MM叫到我的电脑旁,“来把下面这条命令打进去,这是个练习打(Pian)符(ni)号(de)的 ...

  8. JavaScript学习心得（四）

    条件语句 任何事物非真即假. 在JavaScript中,条件判断以下情况为假: false NaN 0 空串 null undefined 在使用相等运算符时,建议将数字写在相等运算符的左边.全等比较 ...

  9. VC皮肤库之duilib

    首先是个国产的开源 的,directui 界面库,开放,共享,惠众,共赢,遵循bsd协议,可以免费用于商业项目,目前支持Windows 32 .Window CE.Mobile等平台. Duilib ...

  10. c++清除输入缓冲区之 sync() vs ignore()

    最近在写程序的时候总是不注意输入缓冲区内是否还有东西,导致出现了一些异常,调试了半天.所以来上一贴,学习注意,引以为戒! http://blog.chinaunix.net/uid-21254310- ...