【HNOI 2016】网络

Problem

Description

一个简单的网络系统可以被描述成一棵无根树。每个节点为一个服务器。连接服务器与服务器的数据线则看做一条树边。两个服务器进行数据的交互时，数据会经过连接这两个服务器的路径上的所有服务器（包括这两个服务器自身）。由于这条路径是唯一的，当路径上的某个服务器出现故障，无法正常运行时，数据便无法交互。此外，每个数据交互请求都有一个重要度，越重要的请求显然需要得到越高的优先处理权。

现在，你作为一个网络系统的管理员，要监控整个系统的运行状态。系统的运行也是很简单的，在每一个时刻，只有可能出现下列三种事件中的一种：

1. 在某两个服务器之间出现一条新的数据交互请求；
2. 某个数据交互结束请求；
3. 某个服务器出现故障。

系统会在任何故障发生后立即修复。也就是在出现故障的时刻之后，这个服务器依然是正常的。但在服务器产生故障时依然会对需要经过该服务器的数据交互请求造成影响。

你的任务是在每次出现故障时，维护未被影响的请求中重要度的最大值。

注意：如果一个数据交互请求已经结束，则不将其纳入未被影响的请求范围。

Input Format

第一行两个正整数 \(n, m\)，分别描述服务器和事件个数。服务器编号是从 \(1\) 开始的，因此 \(n\) 个服务器的编号依次是 \(1, 2, 3, \cdots ,n\)。

接下来 \(n-1\) 行，每行两个正整数 \(u, v\)，描述一条树边。\(u\) 和 \(v\) 是服务器的编号。

接下来 \(m\) 行，按发生时刻依次描述每一个事件；即第 \(i\) 行（\(i = 1, 2, 3, \cdots , m\)）描述时刻 \(i\) 发生的事件。每行的第一个数 \(\text{type}\) 描述事件类型，共三种类型：

1. 若 \(\text{type} = 0\)，之后有三个正整数 \(a, b, v\)，表示服务器 \(a, b\) 之间出现一条重要度为 \(v\) 的数据交互请求；

2. 若 \(\text{type} = 1\)，之后有一个正整数 \(t\)，表示时刻 \(t\) （也就是第 \(t\) 个发生的事件）出现的数据交互请求结束；

3. 若 \(\text{type} = 2\)，之后有一个正整数 \(x\)，表示服务器 \(x\) 在这一时刻出现了故障。对于每个 \(\text{type}\) 为 \(2\) 的事件，就是一次询问，即询问「当服务器 \(x\) 发生故障时，未被影响的请求中重要度的最大值是多少？」

注意：可能有某个服务器自身与自身进行数据交互的情况。

Output Format

对于每个 \(\text{type} = 2\) 的事件，即服务器出现故障的事件，输出一行一个整数，描述未被影响的请求中重要度的最大值。

如果此时没有任何请求，或者所有请求均被影响，则输出 \(-1\)。

Sample

Input

13 23
1 2
1 3
2 4
2 5
3 6
3 7
4 8
4 9
6 10
6 11
7 12
7 13
2 1
0 8 13 3
0 9 12 5
2 9
2 8
2 2
0 10 12 1
2 2
1 3
2 7
2 1
0 9 5 6
2 4
2 5
1 7
0 9 12 4
0 10 5 7
2 1
2 4
2 12
1 2
2 5
2 3

Output

-1
3
5
-1
1
-1
1
1
3
6
7
7
4
6

Explanation

Explanation for Input

样例给出的树如下所示：

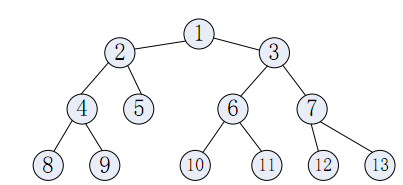
解释其中的部分询问；下面的解释中用 \((a, b ; t, v)\) 表示在 \(t\) 时刻出现的服务器 \(a\) 和 \(b\) 之间的重要度为 \(v\) 的请求：

对于第一个询问（在时刻 \(1\)），此时没有任何请求，输出 \(-1\)。

对于第四个询问（在时刻 \(6\)），此时有两条交互 \((8, 13 ; 2, 3), (9, 12 ; 3, 5)\)，所有询问均经过 \(2\) 号服务器，输出 \(-1\)。

对于第五个询问（在时刻 \(8\)），此时有三条交互 \((8, 13 ; 2, 3),(9, 12 ; 3, 5), (10, 12 ; 7, 1)\)，只有交互 \((10, 12 ; 7, 1)\) 没有经过 \(2\) 号服务器，因此输出其重要度 \(1\)。

对于最后一个询问（在时刻 \(23\)），此时有三条交互 \((9, 5 ; 12, 6), (9, 12 ; 16, 4), (10, 5 ; 17, 7)\)。当\(3\)号服务器出现故障时，只有交互 \((9, 5 ; 12, 6)\) 没有经过 \(3\) 号服务器，因此输出 \(6\)。

Range

\(2 \leq n \leq 10^5 , 1 \leq m \leq 2 \times 10^5\)，其他的所有输入值不超过 \(10^9\) 。

Algorithm

树状数组，整体二分

Mentality

一道裸得不能再裸的整体二分 \(QwQ\) 。

我们将所有操作和询问丢到序列里整体二分，每次二分一个值 \(mid\) ，然后将所有 \(\ge mid\) 的路径都丢到树状数组里，如果一个询问点被所有 \(\ge mid\) 的路径经过，那么答案肯定 \(\le mid\) ，丢到左边递归，否则丢到右边。

那如何用树状数组判断一个点被多少符合要求的路径经过呢？这是由两个很基础的结论组成的：

• 对于一条路径，我们进行树上差分，在 \(u,v\) 位置的差分数组上 \(+1\) ，\(lca\) 和 \(fa[lca]\) 处 \(-1\) ，然后统计子树和，每个点得到的子树和就是经过它的路径条数。

• 处理出 \(dfs\) 序后，任意一个点 \(i\) 的子树内的 \(dfs\) 序肯定是 \(dfn[i]\sim dfn[i]+size[i]-1\) 之间的那些值。所以我们将子树和利用 \(dfs\) 序作为下标转化成区间和统计即可。

完毕。

真是水得不行。

Code

#include <cstdio>
#include <iostream>
using namespace std;
int n, m, cnt, opt, head[100001], nx[200001], to[200001];
int fa[100001][18], size[100001], deep[100001], d[100001];
int mid, now, c[200001], num[200001], tmp[200001], Ans[200001];
struct Que {
  int u, v, w, id, type;
} q[200001], q1[200001], q2[200001];
void addroad(int u, int v, int d) {
  nx[d] = head[u], to[d] = v;
  head[u] = d;
}
void build(int x, int pa) {
  size[x] = 1, fa[x][0] = pa, deep[x] = deep[pa] + 1, d[x] = ++cnt;
  for (int i = 1; i <= 17; i++) fa[x][i] = fa[fa[x][i - 1]][i - 1];
  for (int i = head[x]; i; i = nx[i])
    if (to[i] != pa) {
      build(to[i], x);
      size[x] += size[to[i]];
    }
}
int get_lca(int u, int v) {
  if (deep[u] < deep[v]) swap(u, v);
  for (int i = 17; i >= 0; i--)
    if (deep[fa[u][i]] >= deep[v]) u = fa[u][i];
  for (int i = 17; i >= 0; i--)
    if (fa[u][i] != fa[v][i]) u = fa[u][i], v = fa[v][i];
  return u == v ? u : fa[u][0];
}
void add(int k, int x) {
  if (!k) return;
  k = d[k];
  for (int i = k; i <= n; i += i & -i) c[i] += x;
}
int query(int k) {
  int ans = 0;
  for (int i = k; i > 0; i -= i & -i) ans += c[i];
  return ans;
}
void Add(int u, int v, int x) {
  int lca = get_lca(u, v);
  add(u, x), add(v, x);
  add(lca, -x), add(fa[lca][0], -x);
  now += x;
}
void Solve(int L, int R, int l, int r) {
  if (L > R) return;
  if (l == r) {
    for (int i = L; i <= R; i++)
      if (q[i].type == 2) Ans[q[i].id] = l;
    return;
  }
  mid = (l + r) >> 1, now = 0;
  for (int i = L; i <= R; i++)
    if (q[i].type != 2 && q[i].w >= mid)
      Add(q[i].u, q[i].v, q[i].type == 1 ? -1 : 1);
    else if (q[i].type == 2)
      num[i] = now,
      tmp[i] = query(d[q[i].u] + size[q[i].u] - 1) - query(d[q[i].u] - 1);
  int len1 = 0, len2 = 0;
  for (int i = L; i <= R; i++) {
    if (q[i].type != 2) {
      if (q[i].w >= mid)
        Add(q[i].u, q[i].v, q[i].type == 1 ? 1 : -1), q2[++len2] = q[i];
      else
        q1[++len1] = q[i];
    } else if (tmp[i] == num[i])
      q1[++len1] = q[i];
    else
      q2[++len2] = q[i];
  }
  for (int i = 1; i <= len1; i++) q[L + i - 1] = q1[i];
  for (int i = 1; i <= len2; i++) q[L + len1 + i - 1] = q2[i];
  Solve(L, L + len1 - 1, l, mid);
  Solve(L + len1, R, mid + 1, r);
}
int main() {
  cin >> n >> m;
  int u, v;
  for (int i = 1; i < n; i++) {
    scanf("%d%d", &u, &v);
    addroad(u, v, i), addroad(v, u, i + n);
  }
  build(1, 0);  //建树，处理出树上信息
  cnt = 0;
  for (int i = 1; i <= m; i++) {
    scanf("%d", &opt);
    q[i].type = opt;
    if (opt == 0) scanf("%d%d%d", &q[i].u, &q[i].v, &q[i].w);
    if (opt == 1) {
      scanf("%d", &u);
      q[i].u = q[u].u, q[i].v = q[u].v, q[i].w = q[u].w;
    }
    if (opt == 2) scanf("%d", &q[i].u), q[i].id = ++cnt;
  }
  Solve(1, m, 0, 1e9 + 1);  //二分上界为最大权值 +1
  for (int i = 1; i <= cnt; i++)
    if (!Ans[i])
      printf("-1\n");
    else
      printf("%d\n", Ans[i] - 1);  //因为最后二分出的肯定不包括那条不经过的最大权值，所以二分得到的答案必定为
                                   //ans+1 ，还要减掉
}