ZJNU 2136 - 会长的正方形

对于n*m网格

取min(n,m)作为最大的正方形边长

则答案可以表示成

s=1~min(n,m)

对于一个s*s的正方形

用oblq数组储存有多少四个角都在这个正方形边上的正方形

以4*4为例

除了4*4自身外，四个角在边上的正方形还有

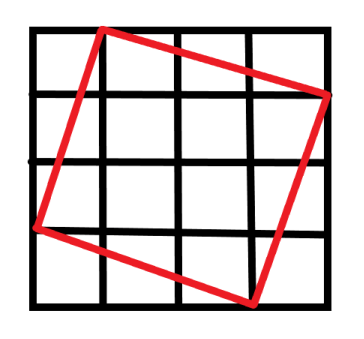
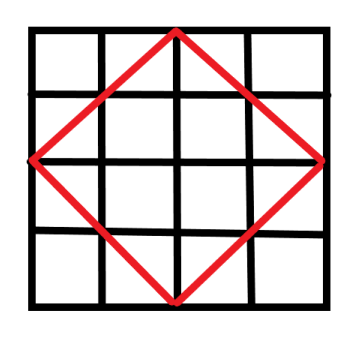
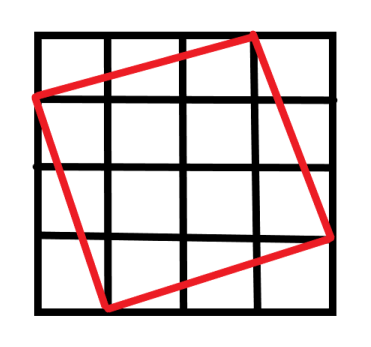
所以4*4网格最多可以有4种正方形存在

推出s*s网格最多可以有s种正方形存在

单看这些正方形在网格上侧的点所在位置

可以发现这种“斜正方形”共有s-1种情况

且每个正方形的边长为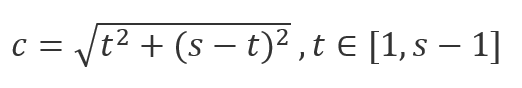

因为S=c^2

所以每个正方形面积为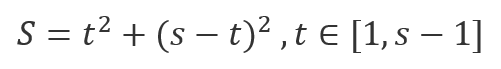

取和，加上原本的面积s*s，存放在oblq[s]内便于引用

然后考虑组合情况

对于一个n*m的网格，里面可以组合出(n-s+1)*(m-s+1)种s*s的正方形

所以每次数量加上(n-s+1)*(m-s+1)*s

面积加上(n-s+1)*(m-s+1)*oblq[s]

取和即可得到答案

代码多加了个t变量，每次让n和m递减，t递增，意义不变

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=;
ll oblq[];
int main(){
    ios::sync_with_stdio();
    cin.tie();cout.tie();
    ll T,n,m,i,j,t,N,S;
    for(i=;i<=;i++){
        oblq[i]=i*i;
        for(j=;j<i;j++)
            oblq[i]+=j*j+(i-j)*(i-j);
        oblq[i]%=mod;
    }
    cin>>T;
    while(T--){
        cin>>n>>m;
        N=S=;
        t=;
        while(n&&m){
            N=(N+n*m*t)%mod;
            S=(S+n*m*oblq[t])%mod;
            n--;
            m--;
            t++;
        }
        cout<<N<<' '<<S<<endl;
    }
 
    return ;
}