HZNU-ACM寒假集训Day10小结 单调栈-单调队列

数据结构往往可以在不改变主算法的前提下题高运行效率，具体做法可能千差万别，但思路却是有规律可循

经典问题：滑动窗口  单调队列O（n）

POJ 2823

我开始写的： TLE 说明STL的库还是有点慢

#include<iostream>
#include<cstdio>
#include<string>
#include<algorithm>
#include<queue>
#include<deque>
#include<set>
#include<map>
#include<cmath>
#include<stack>
const double PI = acos(-1.0);
#define INF 0x3f3f3f3f
typedef long long ll;
using namespace std;

struct Deq {
    int idx;
    int w;
};

deque<Deq> q;
deque<Deq> qq;
int Max[];

int main() {
    int n, k;
    int x;
    int cnt = ;
    scanf("%d%d", &n, &k);
    for (int i = ; i < n; i++) {
        if (i < k) {
            scanf("%d", &x);
            Deq qqq;
            qqq.idx = i;
            qqq.w = x;
            if (q.empty()) q.push_back(qqq);
            if (qq.empty()) qq.push_back(qqq);
            else {
                while (!q.empty() && q.back().w < x) q.pop_back();
                q.push_back(qqq);
                while (!qq.empty() && qq.back().w > x) qq.pop_back();
                qq.push_back(qqq);
            }
            if (i == k - ) {
                printf("%d", qq.front().w);
                Max[cnt++] = q.front().w;
            }
        }
        else {
            scanf("%d", &x);
            Deq qqq;
            qqq.idx = i;
            qqq.w = x;
            if (q.empty()) q.push_back(qqq);
            if (qq.empty()) qq.push_back(qqq);
            else {
                while (!q.empty() && q.back().w < x) q.pop_back();
                q.push_back(qqq);
                while (!qq.empty() && qq.back().w > x) qq.pop_back();
                qq.push_back(qqq);
            }
            while (q.front().idx < i +  - k) q.pop_front();
            while (qq.front().idx < i +  - k) qq.pop_front();
            printf(" %d", qq.front().w);
            Max[cnt++] = q.front().w;
        }
    }
    printf("\n");
    for (int i = ; i < cnt; i++) {
        i ==  ? printf("%d", Max[i]) : printf(" %d", Max[i]);
    }
    return ;
}

洛谷题解：

直接用下标存进队列 手写双端队列

#include<iostream>
#include<cstdio>
#include<string>
#include<algorithm>
#include<queue>
#include<deque>
#include<set>
#include<map>
#include<cmath>
#include<stack>
const double PI = acos(-1.0);
#define INF 0x3f3f3f3f
typedef long long ll;
using namespace std;

const int maxn = ;
int n, m;
int q1[maxn], q2[maxn];
int a[maxn];

void Min_que() {
    int h = ;     //head
    int t = ;     //tail
    for (int i = ; i <= n; i++) {
        while (h <= t && q1[h] + m <= i)    h++;
        while (h <= t && a[i] < a[q1[t]]) t--;
        q1[++t] = i;
        if (i >= m) printf("%d ", a[q1[h]]);
    }
    printf("\n");
}

void Max_que() {
    int h = ;
    int t = ;
    for (int i = ; i <= n; i++) {
        while (h <= t && q2[h] + m <= i) h++;
        while (h <= t && a[i] > a[q2[t]]) t--;
        q2[++t] = i;
        if (i >= m) printf("%d ", a[q2[h]]);
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = ; i <= n; i++) scanf("%d", &a[i]);
    Min_que();
    Max_que();
    return ;
}

单调栈：

#include<iostream>
#include<cstdio>
#include<string>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#include<cmath>
#include<stack>
const double PI = acos(-1.0);
#define INF 0x3f3f3f3f
typedef long long ll;
using namespace std;

struct S {
    int idx;
    int w;
};
stack<S> s;
int a[];
vector<int> f;

int main() {
    int n;
    scanf("%d", &n);
    for (int i = ; i < n; i++) scanf("%d", &a[i]);
    for (int i = n - ; i >= ; i--) {
        if (i == n - ) {
            f.push_back();
            s.push({ i,a[i] });
        }
        else {
            if (s.empty()) {
                f.push_back();
                s.push({ i,a[i] });
            }
            else {
                while (!s.empty()&&s.top().w <= a[i]) s.pop();
                if (!s.empty()) f.push_back(s.top().idx+);
                else f.push_back();
                s.push({ i,a[i] });
            }
        }
    }
    for (auto it = f.rbegin(); it != f.rend(); it++) {
        if (it == f.rbegin()) printf("%d", *it);
        else printf(" %d", *it);
    }
    return ;
}

HDU 1506

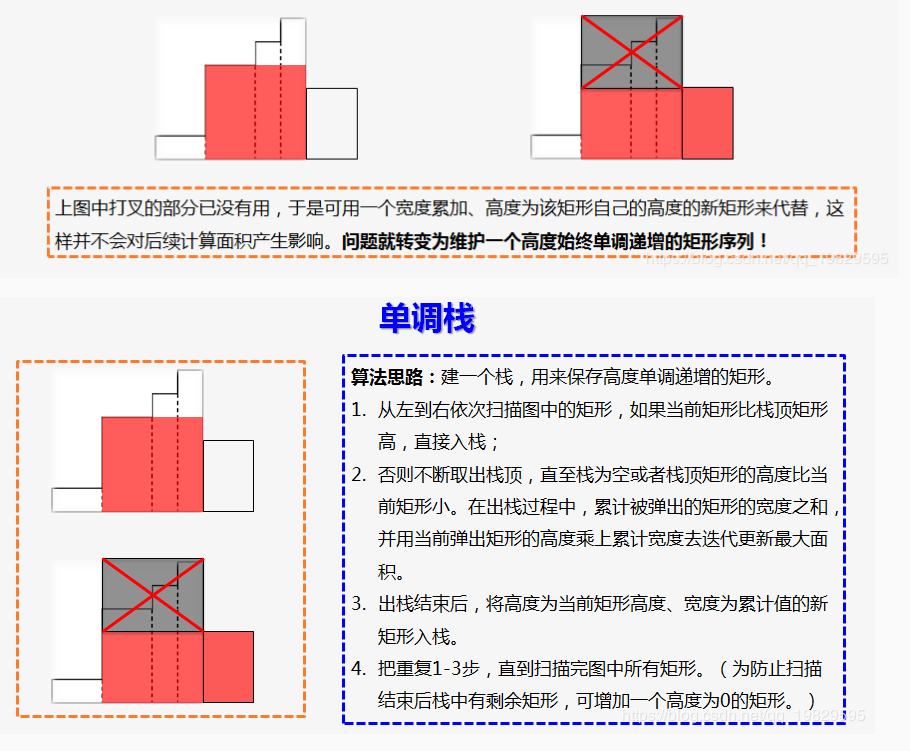
题目题意:题目给了n个矩形的高度，问最大连续矩形的公共面积（底乘以这段连续矩形中最短的高度)，每个矩形的底是1

感觉有点像贪心，想了很久没想出单调栈的做法 事实上需要维护一个递增的矩形，每次出栈维护最大值

#include<iostream>
#include<cstdio>
#include<string>
#include<algorithm>
#include<queue>
#include<deque>
#include<set>
#include<map>
#include<cmath>
#include<stack>
const double PI = acos(-1.0);
#define INF 0x3f3f3f3f
typedef long long ll;
using namespace std;

const int maxn = ;
int a[maxn];
int s[maxn], w[maxn];

ll ans;

int main() {
    int n;
    while (scanf("%d", &n) != EOF) {
        if (!n) break;
        int p = ;
        ans = ;
        for (int i = ; i <=n; i++) scanf("%d", &a[i]);
        a[n+] = ;                                      //注意设置a[0]=0,a[n+1]=0,因为最后一个也可能出栈
        for (int i = ; i <= n+; i++) {
            if (a[i] > s[p]) s[++p] = a[i], w[p] = ;  //维护单调递增的栈
            else {
                int wid = ;
                while (s[p] > a[i]) {
                    wid += w[p];
                    ans = max(ans, (ll)wid * s[p]);     //core
                    p--;
                }
                s[++p] = a[i];
                w[p] = wid + ;
            }
        }
        printf("%lld\n", ans);
    }
    return ;
}

POJ 3494 求一个0-1矩阵中全为1的最大子矩阵。

#include<iostream>
#include<cstdio>
#include<string>
#include<algorithm>
#include<queue>
#include<deque>
#include<set>
#include<map>
#include<cmath>
#include<stack>
const double PI = acos(-1.0);
#define INF 0x3f3f3f3f
typedef long long ll;
using namespace std;

const int maxn = ;
int mp[maxn][maxn];
int h[maxn][maxn];
int L[maxn], R[maxn], st[maxn];

int main() {
    int n, m;
    while (scanf("%d%d", &n, &m) != EOF) {
        for (int i = ; i < n; i++) {
            for (int j = ; j < m; j++) {
                scanf("%d", &mp[i][j]);
            }
        }
        for (int i = ; i < m; i++) {
            int high = ;
            for (int j = n - ; j >= ; j--) {
                if (mp[j][i])  high++;
                else high = ;
                h[j][i] = high;
            }
        }
        int ans = ;
        for (int i = ; i < n; i++) {
            int pos = ;
            for (int j = ; j < m; j++) {
                while (pos >  && h[i][st[pos - ]] >= h[i][j]) pos--;
                L[j] = pos ==  ?  : st[pos - ] + ;
                st[pos++] = j;
            }
            pos = ;
            for (int j = m - ; j >= ; j--) {
                while (pos >  && h[i][st[pos - ]] >= h[i][j]) pos--;
                R[j] = pos ==  ? m -  : st[pos - ] - ;
                st[pos++] = j;
            }
            for (int j = ; j < m; j++) {
                ans = max(ans, h[i][j] * (R[j] - L[j] + ));
            }
        }
        printf("%d\n", ans);
    }
    return ;
}