迷宫问题求解——C++

迷宫问题思路

根据昨天的博客，有如下几种解决方案

1. 克鲁斯卡尔 ，为避免死循环，需要设定优化路径的次数。
2. Prim，为避免死循环，需要设定优化路径的次数，暂定200次。
3. BFS ， 实现简单，无死循环。
4. DFS , 实现简单，无死循环，复杂度较低。
5. 动态规划，实时根据权重调整方向，目前看来最合适的解决方案。需要以数据证明。

综上，本次优先选择BFS，首先不存在死循环的风险，其次算法复杂度较低，容易理解且实现。适合初步练手。

一. 思路及程序算法

首先建立迷宫，将其看作点位矩阵，先把墙堆起来，剩下的就是路。

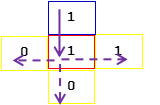
而每个点都有四个方向（上、下、左、有），每个方向上都对应一个点。在这四个点中，有一个点是当前站立点的“上一个点”，另外三个点是当前站立点的“下一个点”，如图1.1所示，红色框为当前站立点，蓝色框为“上一个点”，黄色框为三个“下一个点”。

图1.1站立点的四个方向

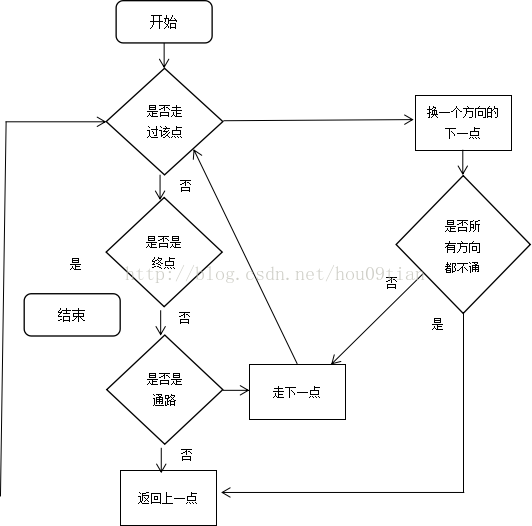
当前站立点有三种状态，分别是“终点”、“通路”和“死路”。如果当前站立点是“终点”，则停止搜索；如果当前站立点是“通路”，则向下继续走；如果当前站立点是“死路”，则要向回走，然后搜索其它路径。其流程如图1.2所示。

图1.2判断迷宫路径流程图

二. 实现

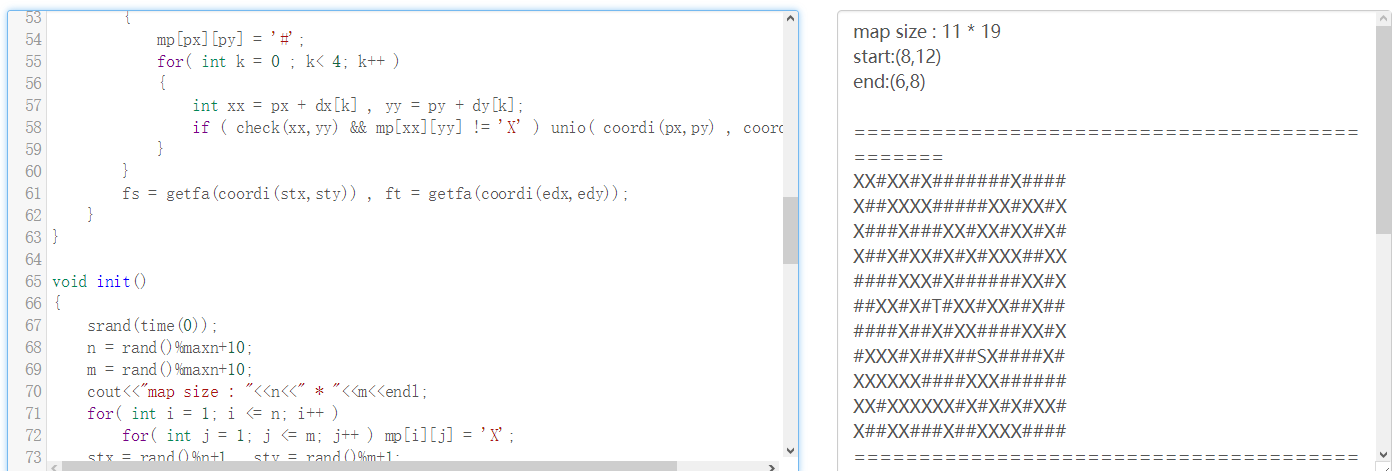
实现效果如图2.1所示：

图2.1 BFS迷宫求解实现图

---

BFS迷宫求解实现代码如下：

#include <bits/stdc++.h>
using namespace std;
#define coordi(x,y) ( m*(x-1)+y )
const int maxn = 30;
const int dx[] = {0,0,1,-1};
const int dy[] = {1,-1,0,0};

int mp[maxn+10][maxn+10];
int nxtx[maxn+10][maxn+10];
int nxty[maxn+10][maxn+10];
bool vis[maxn+10][maxn+10];
int fa[(maxn+10)*(maxn+10)];
int n , m;
int stx , sty , edx , edy;

inline int check( int x , int y )
{
    return 1<=x && x<=n && 1<=y && y<=m;
}
inline void print_map()
{
    puts("\n==============================================");
    for( int i = 1; i <= n; i++ )
    {
        for( int j = 1; j <= m; j++ )
            printf("%c",mp[i][j]);
        putchar('\n');
    }
    puts("==============================================");
}
// 并查集
int getfa( int x )
{
    return x==fa[x]?x:fa[x] = getfa(fa[x]);
}
void unio( int a , int b )
{
    int fx = getfa(a) , fy = getfa(b);
    if ( fx != fy ) fa[fx] = fy;
}
// 并查集

void connect()
{
    int t = n*m/3*2;
    for( int i = 1; i <= n*m; i++ ) fa[i] = i;
    int fs = getfa(coordi(stx,sty)) , ft = getfa(coordi(edx,edy));
    while( fs != ft || t > 0 )
    {
        t--;
        int px = rand()%n+1 , py = rand()%m+1;
        if ( mp[px][py] == 'X' )
        {
            mp[px][py] = '.';
            for( int k = 0 ; k< 4; k++ )
            {
                int xx = px + dx[k] , yy = py + dy[k];
                if ( check(xx,yy) && mp[xx][yy] != 'X' ) unio( coordi(px,py) , coordi(xx,yy) );
            }
        }
        fs = getfa(coordi(stx,sty)) , ft = getfa(coordi(edx,edy));
    }
}

void init()
{
    srand(time(0));
    n = rand()%maxn+10;
    m = rand()%maxn+10;
    cout<<"map size : "<<n<<" * "<<m<<endl;
    for( int i = 1; i <= n; i++ )
        for( int j = 1; j <= m; j++ ) mp[i][j] = 'X';
    stx = rand()%n+1 , sty = rand()%m+1;
    edx = rand()%n+1 , edy = rand()%m+1;
    while( abs(edx-stx) + abs(edy-sty) <= 1 ) edx = rand()%n+1 , edy = rand()%m+1;
    mp[stx][sty] = 'S' , mp[edx][edy] = 'T';
    cout<<"start:("<<stx<<","<<sty<<")"<<endl;
    cout<<"end:("<<edx<<","<<edy<<")"<<endl;
    connect();
    print_map();
}

void print_path() // path = '*'  st = S , ed = T   ,  road = . , wall =  X
{
    int x = edx , y = edy;
    while( !( x == stx && y == sty ) )
    {
        mp[x][y] = '*';
        int tx = nxtx[x][y];
        y = nxty[x][y];
        x = tx;
    }
    mp[edx][edy] = 'T';
    print_map();
}

void bfs()
{
    queue< pair<int,int> > q;
    q.push( make_pair(stx,sty) );
    memset(vis,0,sizeof(vis));
    vis[stx][sty] = true;
    while( !q.empty() )
    {
        pair<int,int> temp = q.front();
        q.pop();
        if ( temp.first == edx && temp.second == edy )
        {
            print_path();
            return;
        }
        for( int k = 0; k < 4; k++ )
        {
            int xx = temp.first + dx[k] , yy = temp.second + dy[k];
            if ( !check(xx,yy) || vis[xx][yy] || mp[xx][yy] == 'X' ) continue;
            vis[xx][yy] = 1 , nxtx[xx][yy] = temp.first , nxty[xx][yy] = temp.second;
            q.push( make_pair(xx,yy) );
        }
    }
}

int main()
{
    init();
    bfs();
    return 0;
}

---