CF1661 Educational Codeforces Round 126 (Rated for Div. 2) 题解

感觉，越来越拉胯了，有点难过，明天希望可以好好学习，好好准备考研！八成新的自己我来力！

A Array Balancing

很明显的签到题，要求两个数组各自的相邻项差的绝对值最小，设\(mn=\min(a_i,b_i),mx=\max(a_i,b_i)\)，把\(mn\)丢到在\(a[i]\)，\(mx\)丢到\(b[i]\)即可。唔 和题解的解法不一样（

namo 这不素重点！重点是，为什么这个方法会ac呢？

假设我们已经按照上述方法构造出两组数列，保证了\(\forall i,a_i<b_i\)。

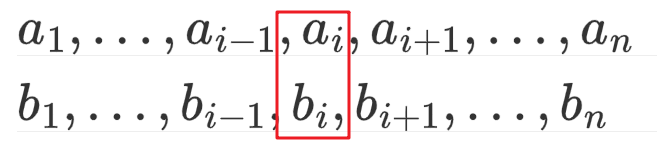
现在，我们把\(b_i\)和\(a_i\)调换位置，那么显然，\(|a_{i-1}-b_i|+|a_{i+1}-b_i|+|b_{i-1}-a_i|+|b_{i+1}-a_i| > |a_{i-1}-a_i|+|a_{i+1}-a_i|+|b_{i-1}-b_i|+|b_{i+1}-b_i|\)。

（前者让更大的数减去了更小的数）

AC代码：

int n;
const int N = 30 + 5;
int a[N], b[N];

void solve(){
	scanf("%d", &n);
	int tmp = 0; ll sm = 0;
	for (int i=1;i<=n;++i){
		scanf("%d", &a[i]);
	}
	for (int i=1;i<=n;++i){
		scanf("%d", &b[i]);
		tmp = min(a[i], b[i]);
		a[i] = a[i] + b[i] - tmp, b[i] = tmp;
	}

	for (int i=1;i<n;++i){
		sm = sm + abs(a[i] - a[i + 1]);
		sm = sm + abs(b[i] - b[i + 1]);
	}
	printf("%lld\n", sm);
}

B Getting Zero

完全没想到BFS（），写完看到friends都在bfs我都惊惹

嗯……我们可以发现一个非常特别的事情，就是模数\(32768=2^{15}\)，那么，任何值都可以通过\(\times2\)操作15次来到达0。因为，\(n\times 2^{15} \equiv 0(\bmod 2^{15})\)嘛。那么这件事就很好办乐，而我就这样直接选了无脑\(2^{15}\times 15\)的暴力，令人感叹（）

时间复杂度：\(O(M\times 15)\)

int n;
const int N = 4e4 + 5, M = 32768;
int a[N], r[N];

void init(){
	memset(r, 0x3f, sizeof(r));

	r[0] = 0, r[M] = 0;
	for (int i=1;i<M;++i){
		int t = 0, cur = i;
		while (cur % M != 0){
			cur <<= 1;
			++t;
		}
		r[i] = t;
	}
	for (int i=M-1;i>0;--i){
		for (int j=1;j<=15;++j){
			r[i] = min(r[i], r[(i + j) % M] + j);
		}
	}
}

int main(void){
	init();
	scanf("%d", &n);
	for (int i=1;i<=n;++i){
		scanf("%d", &a[i]);
		printf(i==n?"%d\n":"%d ", r[a[i]]);
	}

	return 0;
}

C Water the Trees

给树浇水这题，首先要明确一点，就是，1和2这两个数它们其实是可以组成任何数的对吧？并且\(1+1=2\)，也就是2可以用两个1代替。假设\(mx=\max\{a[n]\}\)，其实我们这样就可以明了，浇水到最后树的高度一定都是\(mx\)，或者都是\(mx+1\)。因为，要让所有树都达到某一高度\(h\)，且\(h>mx+1\)的话，我们总能让树们先统一的到达\(mx\)或者\(mx+1\)的高度。

解决了第一个问题，我们要再用聪明的脑瓜子想到（以计算所有树到达\(mx\)为例），这就代表，对于第\(i\)棵树，它的高度是\(h_i\)，那么它需要长大\(r_i=mx-h_i\)那么多。

• 假如\(r_i\)为奇数，那么显然，一定要有个1分给它。
• 如果\(r_i\)是偶数，我们可以一直在偶数天浇水，也可以让\(1+1=2\)，凑出偶数。

OK！那现在怎么算最小天数已经呼之欲出辣，我们先算出\(r_i\)为奇数的个数，我们必须要分给它们一个1，这是我们必定要花的奇数天。奇数-1=偶数，剩下的就可以全部按照偶数计算。这只是一个小小的边界，俺相信剩下的内容大家都会惹。具体步骤可以参见代码（不许吐槽我一模一样的代码粘贴两遍QAQ，我高兴！嘴硬ing）

时间复杂度：\(O(N)\)

AC代码：

int n;
const int N = 3e5 + 5;
ll h[N];

void solve(){
	scanf("%d", &n);
	ll mx, one, two, day;
	ll res = 2e18 + 1LL;
	for (int i=1;i<=n;++i){
		scanf("%lld", &h[i]);
	}
	sort(h + 1, h + 1 + n);
	mx = h[n], one = 0, two = 0;
	for (int i=1;i<=n;++i){
		ll t = mx - h[i];
		if (t & 1){
			++one, two += (t - 1);
		}
		else two += t;
	}
	day = max(0LL, one - 1);
	if (day * 2 >= two){
		res = min(res, day + one);
	}
	else{
		two -= one * 2, day = one * 2;
		if (two % 3 == 0) day += two / 3 * 2;
		else if (two % 3 == 1) day += two / 3 * 2 + 1;
		else day += (two + 2) / 3 * 2;
		res = min(res, day);
	}

	mx = h[n] + 1, one = 0, two = 0;
	for (int i=1;i<=n;++i){
		ll t = mx - h[i];
		if (t & 1){
			++one, two += (t - 1);
		}
		else two += t;
	}
	day = max(0LL, one - 1);
	if (day * 2 >= two){
		res = min(res, day + one);
	}
	else{
		two -= one * 2, day = one * 2;
		if (two % 3 == 0) day += two / 3 * 2;
		else if (two % 3 == 1) day += two / 3 * 2 + 1;
		else day += (two + 2) / 3 * 2;
		res = min(res, day);
	}

	printf("%lld\n", res);
}

D Progressions Covering

好险，差点就屈服写线段树乐（）

显然，我们要做一个贪心，从后往前取，把等差数列们逆向构造出来，这样代码的复杂度是\(O(N^2)\)，显然是会\(TLE\)的（哼哼，我就是直接写然后TLE了的猪鼻）

贴一下\(O(N^2)\)的代码：

int main(void){
	n = read(), m = read();
	ll res = 0, cur = 0, inx = 0;
	for (int i=1;i<=n;++i){
		b[i] = read();
	}

	for (int i=n;i>=1;--i){
		b[i] -= d[i];
		if (b[i] <= 0) continue;
		inx = (i >= m) ? m : i;
		cur = (b[i] + inx - 1) / inx;
		for (int j=1;j<inx&&i-j>0;++j){
			d[i - j] += cur * (inx - j);
		}
		res += cur;
	}

	printf("%lld\n", res);

	return 0;
}

那么，还有什么方法呢？也许我们可以直接考虑一个等差数列什么时候出现，以及什么时候消失？显然，如果\(b[i]>0\)时，我们就不得不构造一个等差数列来消除\(b[i]\)了，而在\(i-inx\)的那个位置，魔法消失了，\(b[i-inx]\)不需要再得到在\(i\)构造的等差数列的贡献了。

嗯……总之，对于这题，我们其实可以把他们看做若干个等差数列合并的情况，最后的那个尾项逐渐衰减，每次衰减公差之和，再用另一个数组\(r[n]\)，记录每个等差数列能控制的最远的地方，那么这题也就结束了。

时间复杂度：\(O(N)\)

int n, m;
const int N = 3e5 + 5;
ll b[N], r[N];

ll read(){
	ll x = 0, f = 1; char ch;
	do{ch=getchar();if(ch=='-') f=-1;}while (ch<'0' || ch>'9');
	do{x=x*10+ch-48;ch=getchar();}while (ch>='0' && ch<='9');
	return x * f;
}

int main(void){
	n = read(), m = read();
	ll res = 0, cur = 0, inx = 0, all = 0, d = 0;
	for (int i=1;i<=n;++i){
		b[i] = read();
	}

	for (int i=n;i>=1;--i){
		all -= d;  // 去掉当前公差
		d -= r[i]; // 去掉用完的公差
		b[i] -= all;
		if (b[i] <= 0) continue;
		inx = (i >= m) ? m : i;
		cur = (b[i] + inx - 1) / inx;
		r[i - inx] += cur;
		all += cur * inx;
		d += cur;
		res += cur;
	}

	printf("%lld\n", res);

	return 0;
}

总体来说，这个教育场不是太难？方法都比较巧妙，但是边界也要稍微想下。wwww现在才写这玩意的题解，应该没人看吧

不过我才不在意会不会有人看呢（）