Educational Codeforces Round 145 (Rated for Div. 2)C. Sum on Subarrays（构造）

很意思的一道构造题

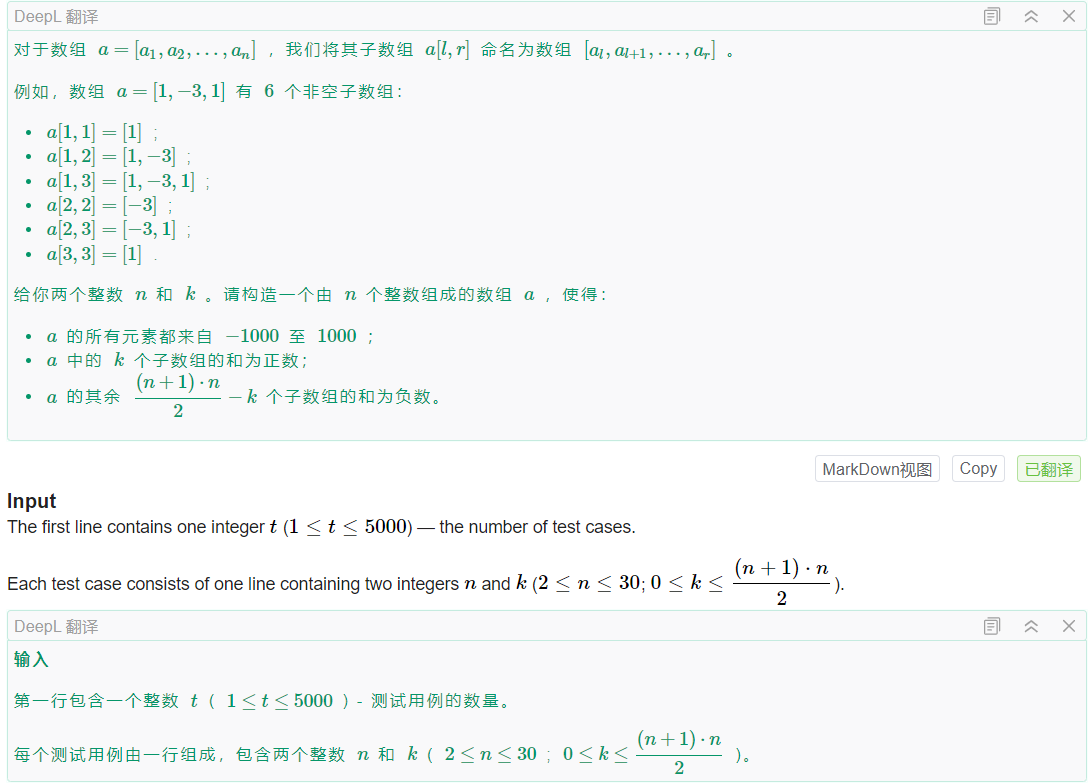
题意：给一个\(n、k\)，让构造长度为n的数组满足，子数组为整数的个数为k个，负数的为\(k-(n+1)* n/2\),每个数的范围为\([-1000,1000]\)

这种构造题可以考虑就是前一段可以一直用一样的、最小的。

我们观察可以发现\(k+k-(n+1)* n/2= (n+1)* n/2\)

也就是所有子数组的个数，换句话说子数组不能有0。

这样我们很容易考虑用很小的一个负数和一个很小的正数去构造

这里我用的是\(1\)和\(-1000\)

我们先考考虑一下前一段是p个1，后面全是-1000的情况这样我们得到的正数组有\(\frac{(p+1) * p}{2}个\)

当\(k=\frac{(p+1) * p}{2}\)时，自然皆大欢喜

当\(k>=\frac{(p+1) * p}{2}\)时，我们考虑一下剩下的\(k-\frac{(p+1) * p}{2}\)该如何臭凑出来，能增加p吗？，当p+1，我们会增加p+1个正数组，这是不行的，我们考虑的p的最大满足\(k>=\frac{(p+1) * p}{2}\)的p，也就是说缺少的正数组个数是在\([1,p]\)

我们可以选择前面p个1中的一个将其变为1000，\(p+1\)处的-1000遍为500，这样我们就可以添加\([1,p]\)个正数组，哪个位置的1变为1000呢？

我们可以找一下规律



弄清楚上面的事情，代码就很简单了，我们只需要而分出最后一个满足条件的p然后按照上面的构造方法放数即可

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define pll pair<long long, long long>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back

using namespace std;

const int N=5e3+10,mod=100003,inf=(1ull<<63)-1;
int n,m,k;
int vis[N],d[N];
int a[1010],b[1010];

void solve()
{
	cin>>n>>k;
	int l=0,r=n;
	while(l<r){
		int mid=(l+r+1)>>1;
		if(mid*(mid+1)/2<=k)	l=mid;
		else	r=mid-1;
	}
	if(l*(l+1)/2==k){
		rep(i,1,l)	cout<<1<<' ';
		rep(i,l+1,n){
			if(i==l+1)	cout<<-500<<' ';
			else cout<<-1000<<' ';
		}
		cout<<endl;
	}else{
		int d=k-(l*(l+1))/2;
		rep(i,1,l){
			if(i==d)	cout<<1000<<' ';
			else	cout<<1<<' ';
		}
		rep(i,l+1,n){
				if(i==l+1)	cout<<-500<<' ';
				else cout<<-1000<<' ';
			}
		cout<<endl;
	}
}

signed main(){
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//   	freopen("1.in", "r", stdin);
  	int _;
	cin>>_;
	while(_--)
	solve();
	return 0;
}