bzoj 1038 瞭望塔 半平面交+分段函数

题目大意

给你一座山，山的形状在二维平面上为折线

给出\((x_1,y_1),(x_2,y_2)...(x_n,y_n)\)表示山的边界点或转折点

现在要在\([x_1,x_n]\)(闭区间)中选择一个点中建立瞭望塔

要求瞭望塔能看到山的任意一个地方

求满足条件的瞭望塔最矮能多矮

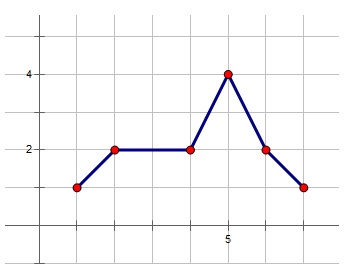
样例如图

分析

对于一个山坡，它能被看到，当且仅当在瞭望塔在山坡对应的直线上方

可以理解为半平面交

也可以像\(~\) 水平可见直线 \(~\)那样理解

由于建的区间还有要限制在\([x_1,x_n]\)

我们额外加两个半平面

搞出来图如下



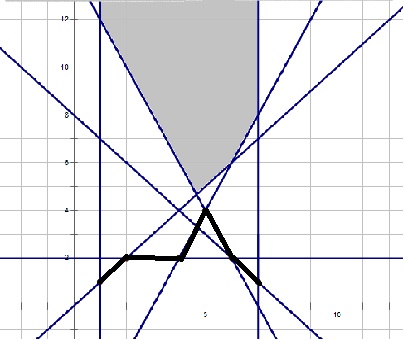
其实发现跟\(~\) 水平可见直线\(~\) 差不多，求出来的半平面交是一个下凸壳

我们假如要在x的位置建瞭望塔

瞭望塔塔底固定了,那么我们就要式瞭望塔塔顶最矮

那一定是在半平面交中\(x\)对应的值

可以发现，这tm就是个分段的一次函数，分段的位置在山转折处/半平面交转折处

对于每段，函数的极点在最左或最右（这不是显然的吗？我怎么想了10分钟？）

枚举一下就好了（如果数据大的话好像要二分找）

做法

求f(x)可以用斜率

之前直线的向量存法P+tv中v向量的斜率=原函数斜率

solution

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <cmath>
#include <algorithm>
using namespace std;
typedef double db;
const db INF=1e30;
const int M=307;

inline int rd(){
	int x=0;bool f=1;char c=getchar();
	for(;!isdigit(c);c=getchar()) if(c=='-') f=0;
	for(;isdigit(c);c=getchar()) x=x*10+c-48;
	return f?x:-x;
}

struct pt{
	db x,y;
	pt(db xx=0.0, db yy=0.0){x=xx;y=yy;}
}p[M];
pt operator +(pt x,pt y){return pt(x.x+y.x,x.y+y.y);}
pt operator -(pt x,pt y){return pt(x.x-y.x,x.y-y.y);}
pt operator *(pt x,db d){return pt(x.x*d,x.y*d);}
pt operator /(pt x,db d){return pt(x.x/d,x.y/d);}
db dot(pt x,pt y){return x.x*y.x+x.y*y.y;}
db det(pt x,pt y){return x.x*y.y-x.y*y.x;}
db len(pt x){return sqrt(dot(x,x));}
db dis(pt x,pt y){return len(y-x);}
db area(pt x,pt y,pt z){return det(y-x,z-x);}

struct line{
	pt P,v;
	line(pt PP=pt(),pt vv=pt()){P=PP;v=vv;}
}l[M],s[M];
bool lineleft(line x,line y){
	db tp=det(x.v,y.v);
	return tp>0||((tp==0)&&det(x.v,y.P-x.P)>0);
}
bool ptright(pt x,line y){return det(y.v,x-y.P)<=0;}
bool parallel(line x,line y){return det(x.v,y.v)==0;}
pt inter(line x,line y){
	pt u=x.P-y.P;
	db t=det(u,y.v)/det(y.v,x.v);
	return x.P+x.v*t;
}

int n,m,top;

bool cmp(line x,line y){
	if(x.v.y==0 && y.v.y==0) return x.v.x<y.v.x;
	if(x.v.y<=0 && y.v.y<=0) return lineleft(x,y);
	if(x.v.y>0 && y.v.y>0) return lineleft(x,y);
	return x.v.y<y.v.y;
}

void hpi(){
	sort(l+1,l+m+1,cmp);
	top=0;
	for(int i=1;i<=m;i++){
		while(top>1&&ptright(inter(s[top-1],s[top]),l[i])) top--;
		s[++top]=l[i];
	}
}

db calc1(pt x){
	for(int i=1;i<top;i++)
	if(inter(s[i],s[i+1]).x>=x.x)
		return (s[i].P.y+s[i].v.y/s[i].v.x*(x.x-s[i].P.x))-x.y;
}

db calc2(pt x){
	for(int i=2;i<=n;i++)
	if(p[i].x>=x.x)
		return x.y-(p[i-1].y+(p[i].y-p[i-1].y)/(p[i].x-p[i-1].x)*(x.x-p[i-1].x));
}

int main(){
	int i;
	n=rd();
	for(i=1;i<=n;i++) p[i].x=rd();
	for(i=1;i<=n;i++) p[i].y=rd();

	for(i=2;i<=n;i++) l[++m]=line(p[i-1],p[i]-p[i-1]);
	l[++m]=line(p[1].x,pt(0,-1));
	l[++m]=line(p[n].x,pt(0,1));

	hpi();

	db ans=INF;
	for(i=1;i<=n;i++)
		ans=min(ans,calc1(p[i]));
	for(i=1;i<top;i++)
		ans=min(ans,calc2(inter(s[i],s[i+1])));

	printf("%.3lf\n",ans);

	return 0;
}