BZOJ 1001 平面图转对偶图

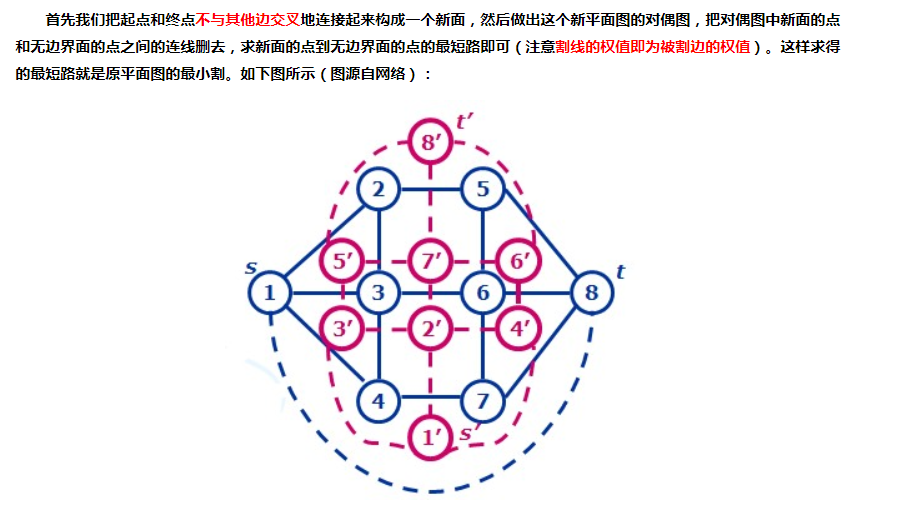
原图的面转成点,原图的边依旧边,只是连接的是两个面.

对偶图的点数=原图的面数 对偶图的边数=原图的边数(如果原边只属于一个面,则它为环边)

#include<bits/stdc++.h>
using namespace std;
const int MAXN = , MAXM = ;
int mindist[MAXN];
bool vis[MAXN];
int to[MAXM << ], nxt[MAXM << ], Head[MAXN], ed = ;
int cost[MAXM << ];
inline void addedge(int u, int v, int c) {
        to[++ed] = v;
        nxt[ed] = Head[u];
        cost[ed] = c;
        Head[u] = ed;
        to[++ed] = u;
        nxt[ed] = Head[v];
        cost[ed] = c;
        Head[v] = ed;
}
inline void read(int &v) {
        v = ;
        char c = ;
        int p = ;
        while (c < '' || c > '') {
                if (c == '-') {
                        p = -;
                }
                c = getchar();
        }
        while (c >= '' && c <= '') {
                v = (v << ) + (v << ) + c - '';
                c = getchar();
        }
        v *= p;
}
struct HeapNode {
        int d, u;
        bool operator < (const HeapNode& rhs) const {
                return d > rhs.d;
        }
} zz;
priority_queue<HeapNode> que;
void Hijkstra(int s) {
        mindist[s] = ;
        memset(vis, , sizeof(vis));
        zz.d = , zz.u = s;
        que.push(zz);
        while (!que.empty()) {
                HeapNode x = que.top();
                que.pop();
                int u = x.u;
                if (vis[u] || mindist[u] != x.d) {
                        continue;
                }
                vis[u] = true;
                for (int v, i = Head[u]; i; i = nxt[i]) {
                        v = to[i];
                        if (mindist[v] > mindist[u] + cost[i]) {
                                mindist[v] = mindist[u] + cost[i];
                                //p[v]=u;
                                zz.d = mindist[v], zz.u = v;
                                que.push(zz);
                        }
                }
        }
}
int n, m;
int getnum(int x, int y, int add) {
        return  (x - ) * (m - ) *  + (y - ) *  + add;
}
int main() {
        int u, v, c;
        read(n), read(m);
        int sum = (n - ) * (m - ) *  + ;
        if (n ==  || m == ) {
                int ans = INT_MAX;
                if (n == ) {
                        for (int i = ; i < m; i++) {
                                read(c);
                                ans = min(ans, c);
                        }
                } else {
                        for (int i = ; i < n; i++) {
                                read(c);
                                ans = min(ans, c);
                        }
                }
                printf("%d\n", ans);
                return ;
        }
        for (int i = ; i <= n; i++) {
                for (int j = ; j <= m - ; j++) {
                        read(c);
                        if (i == ) {
                                addedge(sum, getnum(i, j, ), c);
                        } else if (i == n) {
                                addedge(sum - , getnum(i - , j, ), c);
                        } else {
                                addedge(getnum(i, j, ), getnum(i - , j, ), c);
                        }
                }
        }
        for (int i = ; i <= n - ; i++) {
                for (int j = ; j <= m; j++) {
                        read(c);
                        if (j == ) {
                                addedge(sum - , getnum(i, j, ), c);
                        } else if (j == m) {
                                addedge(sum, getnum(i, j - , ), c);
                        } else {
                                addedge(getnum(i, j, ), getnum(i, j - , ), c);
                        }
                }
        }
        for (int i = ; i <= n - ; i++) {
                for (int j = ; j <= m - ; j++) {
                        read(c);
                        addedge(getnum(i, j, ), getnum(i, j, ), c);
                }
        }
        for (int i = ; i <= sum + ; i++) {
                mindist[i] = 1e9;
        }
        Hijkstra(sum - );
        printf("%d\n", mindist[sum]);
}