P2661 信息传递[最小环+边带权并查集]

题目来源：洛谷

题目描述

有 n 个同学（编号为 1 到 n ）正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象，其中，编号为 i 的同学的信息传递对象是编号为 Ti​ 的同学。

游戏开始时，每人都只知道自己的生日。之后每一轮中，所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象（注意：可能有人可以从若干人那里获取信息， 但是每人只会把信息告诉一个人，即自己的信息传递对象）。当有人从别人口中得知自 己的生日时，游戏结束。请问该游戏一共可以进行几轮？

输入输出格式

输入格式：

共2行。第1行包含1个正整数 n ，表示 n 个人。

输出格式：

1个整数，表示游戏一共可以进行多少轮。

输入输出样例

输入样例#1：

5
2 4 2 3 1

输出样例#1：

3

说明

样例1解释

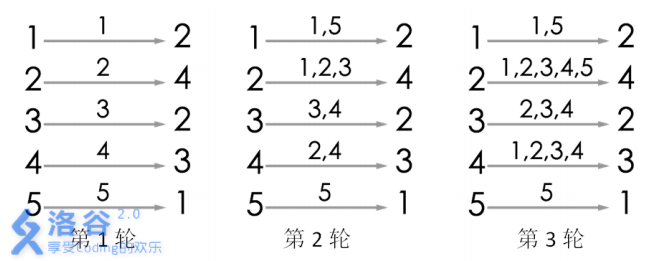
游戏的流程如图所示。当进行完第3 轮游戏后， 4号玩家会听到 2 号玩家告诉他自己的生日，所以答案为 3。当然，第 3 轮游戏后， 2号玩家、 3 号玩家都能从自己的消息来源得知自己的生日，同样符合游戏结束的条件。

对于 30%的数据， n≤200；

对于 60%的数据，n ≤2500；

对于 100%的数据， n≤200000。

解析：

在想了半天之后还是去看了题解，我真tm弱。

写这道题看标签有个并查集，结果实际上是坑人的。这哪里是并查集啊喂？！虽说也是吧，但是与其说是并查集，倒不如说是用并查集这种思想记录一下数据之间的关系。。。

这个关系，其实就是某节点信息当前传递到的节点的位置而已，可以把它看成一条链，我们称其为“信息传递链”。

这道题其实是求最小环。。。其他最小环算法也可以搞定。

---

2019-06-04 更新

咳咳，看来是本蒟蒻见识短浅了，经过几天学习，发现这种并查集叫边带权并查集，它能很好的维护带有传递性的关系。

具体来讲，就是在路径压缩时同步更新某些信息，让每个节点之间的关系得以体现。

这道题可以作为边带权并查集的入门模板，如果要深入学习，建议看看这两道题：P1196 [NOI2002]银河英雄传说 P1197 [JSOI2008]星球大战

---

这道题稍微有点难以理解，因为如果要用并查集做，要稍微做一点转换。

本题所谓的信息传递，实际上每次传递就相当于在有向图中连一条边，在并查集中记录父节点，由于并查集带权，我们开一个数组d[]记录一下就好了。

而当某个节点得知自己的信息时，说明在有向图中构成了一个环。而题目便是要求我们求一个最小环了。

注意不要把前驱和后继搞混了。。。

PS：如果把本题看作一张有向图，那么自始至终这张图都不会出现一个环，因为如果连接任意一个环，之后查找这个环中某一结点的父节点时，就会陷入死循环。

参考代码：

 #include<cstdio>
 #include<iostream>
 #include<cmath>
 #include<cstring>
 #include<ctime>
 #include<cstdlib>
 #include<algorithm>
 #include<queue>
 #include<set>
 #include<map>
 #define N 200010
 using namespace std;
 int fa[N],d[N],ans;
 int get(int x)
 {
     if(x!=fa[x])
     {
         int pre=fa[x];
         fa[x]=get(fa[x]);
         d[x]+=d[pre];//将之前节点到父节点的距离传递
     }
     return fa[x];
 }
 void query(int x,int y)
 {
     int a=get(x),b=get(y);
     if(a!=b)
     {
         fa[a]=b;
         d[x]=d[y]+;//连接一条边
     }
     else
     {
         ans=min(ans,d[x]+d[y]+);//注意此处并没有连成一个环!
     }
 }
 int main()
 {
     int n,x;
     scanf("%d",&n);
     for(int i=;i<=n;i++) fa[i]=i;
     ans=0x7fffffff;
     for(int i=;i<=n;i++){
         scanf("%d",&x);
         query(i,x);
     }
     printf("%d\n",ans);
     return ;
 }

2019-05-26 12:59:29