DS AVL树详解

　　　　先说说二叉搜索树: 是有序的二叉树,根值>左节点值,右节点值>根值。

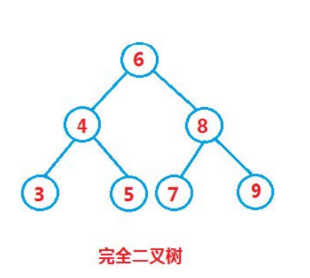
　　　　如果要查找某个值,二叉搜索树和二分查找一样,每进行一次值比较,就会减少一半的遍历区间。

　　　　但是,如果树插入的值一直递增/递减,就会出现这种情况:

　　　　这样,二叉树性能就完全失去了,直接退化成了顺序表,查找效率低下。

　　　　由此,引入了能保持性能最佳的二叉搜索树。

　　　　AVL树: 具有高度平衡的二叉搜索树。

　　　　性质: 1.它的左右子树都是AVL树

　　　　　　  2.左右子树高度差(简称平衡因子)的绝对值不超过1

                  

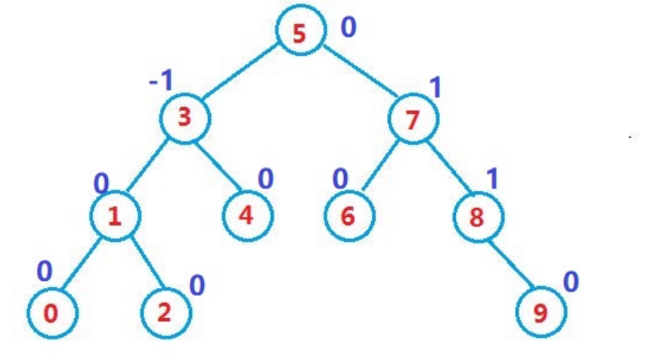
　　　　　　搜索的时间复杂度: O(log2(n))

　　　　　　 AVL树节点　　　　

struct AVLTree{
pair<K,V> kv;
 	AVLTreeNode* left;
 	AVLTreeNode* right;
        AVLTreeNode* parent;

        int bf; //balance factor
};

　　             与二叉搜索树不同的是引入了父节点(方便后面讲的旋转)和平衡因子(保持高度平衡的核心)。

　　　　　　AVL树的插入:

　　　　　　在插入节点后,需要调整平衡:

　　　　　　1.bf更新规则:新增在左 父亲bf-1 ;  新增在右 父亲bf+1

　　　　　　2.持续往祖先更新  如果 祖先bf==0,祖先肯定是从1或者-1变来的,那就说明祖先所在子树的高度不变,停止更新;

　　　　　　　　　　　　　　          祖先|bf|==1,祖先肯定是从0变来的,说明祖先所在子树高度变了,继续往上更新;

　　　　　　　　　　　　　　　　　祖先|bf|==2,祖先肯定是从1或者-1变来的,说明高度已经不平衡了,需要旋转调整;

　　　　　　旋转:

　　　　　　1.左单旋: 新结点插在较高右子树右侧   2 1  

                     

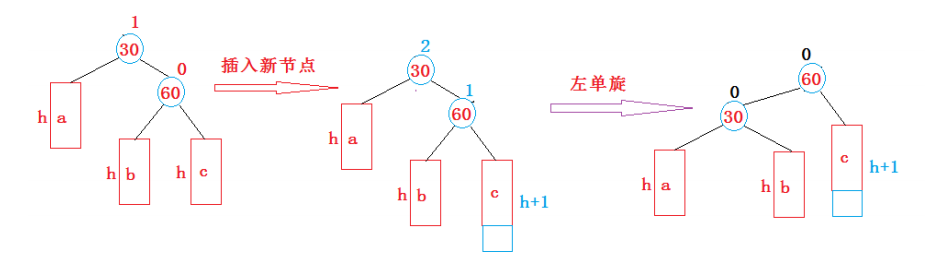
　　　　　　2.右单旋: 新结点插在较高左子树左侧  -2 -1 

                    

　　　　　　3.左右双旋(先左单旋parent,再右单旋g):  新结点插在较高左子树右侧  -2 1 -> -2 -2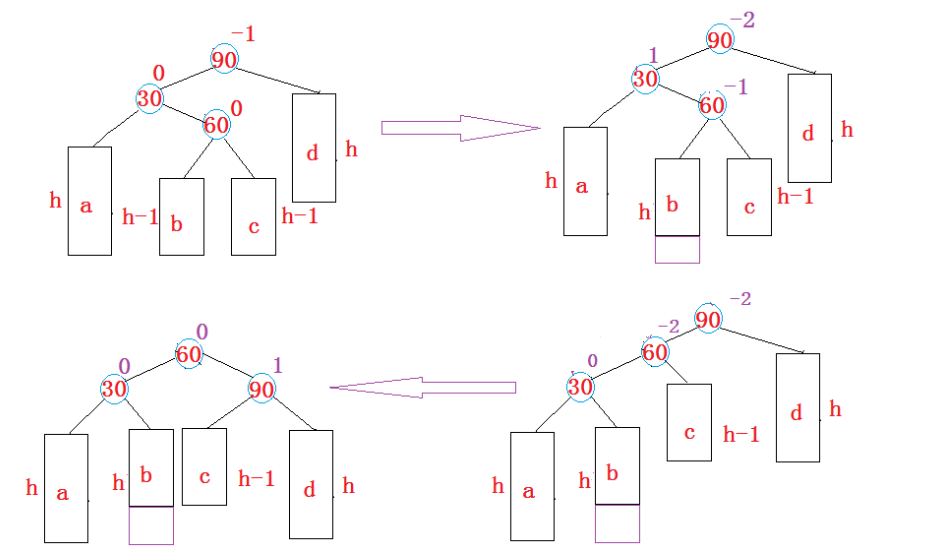                                

　　　　　　4.右左双旋:  新结点插在较高右子树左侧   2 -1 -> 2 2

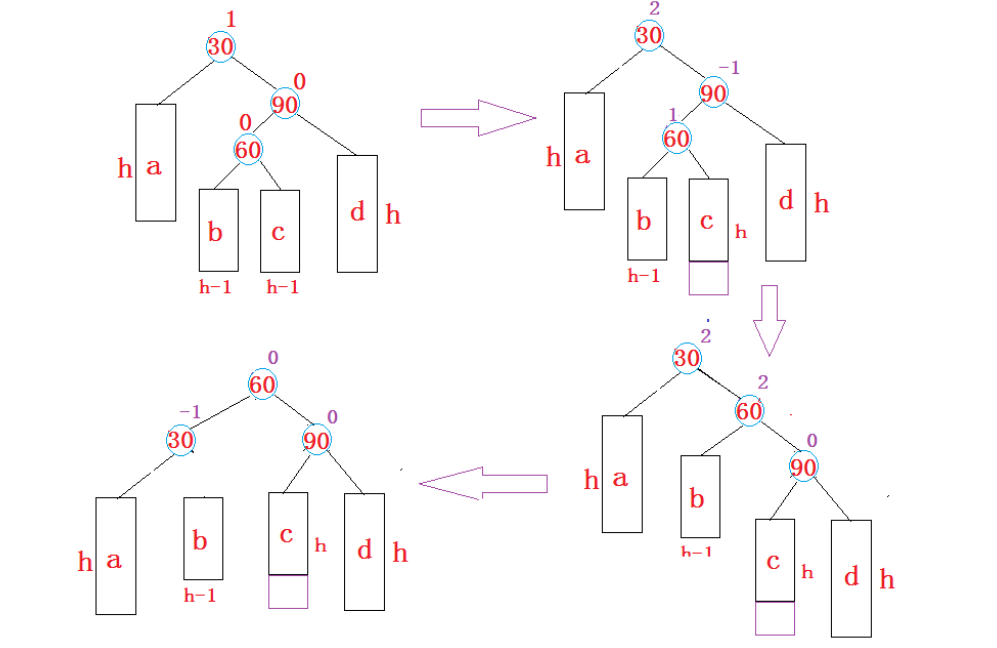
　　　　总结:

　　　   　　1. pParent的平衡因子为2，说明pParent的右子树高，设pParent的右子树的根为pSubR

　　　　　　当pSubR的平衡因子为1时，执行左单旋

　　　　　　当pSubR的平衡因子为-1时，执行右左双旋

　　　　　　2. pParent的平衡因子为-2，说明pParent的左子树高，设pParent的左子树的根为pSubL

　　　　　　当pSubL的平衡因子为-1是，执行右单旋

　　　　　　当pSubL的平衡因子为1时，执行左右双旋

　　　　　　旋转完成后，原pParent为根的子树个高度降低，已经平衡，不需要再向上更新。

 

　　　　　　AVL树旋转代码:

//右单旋
void RotateR(Node* parent)
{
    Node* subL = parnet->left;
    Node* subLR = subL->right;

    //右旋下去,原根左孩子成为新根
    parent->left = subLR;
    if(subLR) //LR不为空,才连接其父亲
    subLR->parent = parent;

    //更新新根与原根的关系
    subL->right = parent;

    //记录原根的父
    Node* ppNode = parent->parent;
    //更新新根与原根的关系
    parent->parent = subL;

    //下面都是因为双向链表带来的问题
    //更新原根父与新根的关系
    //新根就是根节点
    if(ppNode==nullptr)
    {
        root = subL;
        root->parent = nullptr;
    }
    //新根更新与原根父的关系
    else
    {
        if(ppNode->left==parent)
            ppNode->left = subL;
        else
            ppNode->right = subL;  

         subL->parent = ppNode;
    }
    //根据上图,更新部分节点平衡因子
    parent->bf = subL->bf = 0;
}
//左单旋同理
void RotateL(Node* parent);　

//右左双旋
void RotateRL(Node* parent)
{
    Node* subR = parent->right;
    Node* subRL = subR->left;
    int bf = subRL->bf;
    //右左双旋
    RotateR(parent->right);
    RotateL(parent);

    //更新双旋后的bf
    //由于单旋会将bf置0,而双旋有三种情况,需要记录旋转前的新根的bf
    //1.新结点插入后,subRL的bf是0 --- 插入的节点就是subRL
    if(bf == 0)
    {
        parent->bf = subRL->bf = subR->bf = 0;
    }
    //2.新结点插入后,subRL的bf是1  --- 插入的节点在subRL右边
    else if(bf == 1)
    {
        subR->bf = 0;
        parent->bf = -1;
        subRL->bf = 0;
    }
    //3.新结点插入后,subRL的bf是-1  --- 插入的节点在它subRL左边
    else if(bf == -1)
    {
        parent->bf = 0;
        subR->bf = 1;
        subRL->bf = 0;
    }
}
//左右双旋同理
void RotateLR(Node* parnet);

　　　　　　 AVL树插入代码

bool Insert(const pair<K,V>& kv)
{
    //插入结点
    if(root == nullptr)
    {
        root=new Node(kv);
        root->bf = 0;
        return true;
    }
    Node* parent = nullptr;
    Node* cur = root;
    while(cur)
    {
        if(cur->kv.first < kv.first)

        else if(cur->kv.first > kv.first)

        else
            return false;
    }
    cur = new Node(kv);
    //父节点连接插入的结点
    if(parent->kv.first < kv.first)
    {
        parent->right = cur;
        cur->parent = parent;
    }
    else
    {
        ...
    }

    //调平衡
    //1.新增在左 父亲bf-1   新增在右 父亲bf+1
    //2.持续往祖先更新 if 祖先bf == 0,则祖先所在子树高度不变,停止往上更新
    //                if 祖先|bf| == 1,则祖先所在子树高度变了,继续往上更新
    //                if 祖先|bf| == 2,则祖先所在树不平衡,则旋转调整
    //1.更新平衡因子
    while(parent)
    {
        if(cur == parent->right)
            parent->bf++;
        else
            parent->bf--;

        //高度不变,更新完成
        if(parent->bf == 0)
            break;
        //高度变了,继续更新
        else if(abs(parent->bf) == 1)
        {
            cur = parent;
            parent = parent->parent;
        }
        //不平衡,旋转调整
        else if(abs(parent->bf) == 2)
        {
            //判断旋转方式
            if(parent->bf==2)
            {
                if(cur->bf==1)
                    RotateL(parent);
                else if(cur->bf==-1)
                    RotateRL(parent);
            }
            else if(parent->bf==-2)
            {
                if(cur->bf==-1)
                    RotateR(parent);
                else if(cur->bf==1)
                    RotateLR(parent);
            }
            break;
        }
        else
            assert(false);
    }
}

　　　　　　因为引入了bf和双向链表,所以有了很多坑,应该避免以下两点:

　　　　　　1.单旋完成后,注意更新其新根与原根父节点的连接关系

　　　　　　2.双旋完成后,注意根据双旋规律进行bf更新