防线修建 bzoj 2300

防线修建

【问题描述】

近来A国和B国的矛盾激化，为了预防不测，A国准备修建一条长长的防线，当然修建防线的话，肯定要把需要保护的城市修在防线内部了。可是A国上层现在还犹豫不决，到底该把哪些城市作为保护对象呢？又由于A国的经费有限，所以希望你能帮忙完成如下的一个任务：

1.给出你所有的A国城市坐标

2.A国上层经过讨论，考虑到经济问题，决定取消对i城市的保护，也就是说i城市不需要在防线内了

3.A国上层询问对于剩下要保护的城市，修建防线的总经费最少是多少

你需要对每次询问作出回答。注意单位1长度的防线花费为1。

A国的地形是这样的，形如下图，x轴是一条河流，相当于一条天然防线，不需要你再修建

A国总是有两个城市在河边，一个点是(0,0)，一个点是(n,0)，其余所有点的横坐标均大于0小于n，纵坐标均大于0。A国有一个不在(0,0)和(n,0)的首都。

(0,0)，(n,0)和首都这三个城市是一定需要保护的。

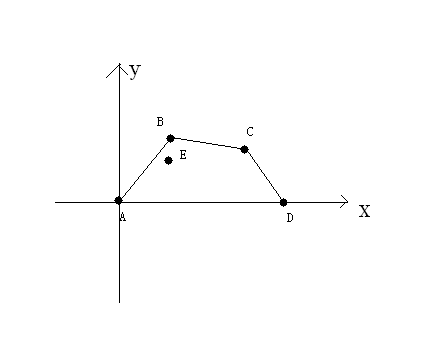
上图中，A,B,C,D,E点为A国城市，且目前都要保护，那么修建的防线就会是A-B-C-D，花费也就是线段AB的长度+线段BC的长度+线段CD的长度

如果，这个时候撤销B点的保护，那么防线变成下图

【输入格式】

第一行，三个整数n,x,y分别表示河边城市和首都是(0,0)，(n,0)，(x,y)。

第二行，一个整数m。

接下来m行，每行两个整数a,b表示A国的一个非首都非河边城市的坐标为(a,b)。

再接下来一个整数q，表示修改和询问总数。

接下来q行每行要么形如1 i，要么形如2，分别表示撤销第i个城市的保护和询问。

【输出格式】

对于每个询问输出1行，一个实数v，表示修建防线的花费，保留两位小数

【样例输入】

4 2 1

2

1 2

3 2

5

2

1 1

2

1 2

2

【样例输出】

6.47

5.84

4.47

【数据范围】

30%的数据m<=1000,q<=1000

100%的数据m<=100000,q<=200000,n>1

所有点的坐标范围均在10000以内, 数据保证没有重点

---

题解：

题意即为支持删点维护一个上凸壳

由于只需要支持删点的操作

那么离线倒序处理，就变为加点操作

若要加入的点在凸包内，那就把它丢掉······

如果这个点在凸包外

分别考虑这个点左右两边的点

向两个方向维护上凸壳

这个过程用set实现

 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<cstdio>
 #include<cmath>
 #include<set>
 using namespace std;
 inline int Get()
 {
     int x = ;
     char c = getchar();
     while('' > c || c > '') c = getchar();
     while('' <= c && c <= '')
     {
         x = (x << ) + (x << ) + c - '';
         c = getchar();
     }
     return x;
 }
 const int me = ;
 int n, m, x, y, e;
 int nu;
 double sum;
 struct dot
 {
     int x, y;
     inline bool operator < (const dot &z) const
     {
         if(x != z.x) return x < z.x;
         return y < z.y;
     }
 };
 dot o;
 dot a[me];
 int flag[me];
 bool vis[me];
 int num[me];
 double ans[me];
 multiset<dot> c;
 inline double Dis(const int &ax, const int &ay, const int &bx, const int &by)
 {
     return sqrt((ax - bx) * (ax - bx) + (ay - by) * (ay - by));
 }
 inline int Cross(const int &ax, const int &ay, const int &bx, const int &by)
 {
     return ax * by - bx * ay;
 }
 inline void Add(dot v)
 {
     multiset<dot>::iterator l = c.upper_bound(v), r = l;
     --l;
     if(Cross((r -> x) - (l -> x), (r -> y) - (l -> y), v.x - (l -> x), v.y - (l -> y)) <= ) return;
     sum -= Dis((l -> x), (l -> y), (r -> x), (r -> y));
     multiset<dot>::iterator now;
     while(l != c.begin())
     {
         now = l;
         --l;
         if(Cross(v.x - (l -> x), v.y - (l -> y), (now -> x) - (l -> x), (now -> y) - (l -> y)) >= )
         {
             ++l;
             break;
         }
         sum -= Dis((now -> x), (now -> y), (l -> x), (l -> y));
         c.erase(now);
     }
     while(true)
     {
         now = r;
         ++r;
         if(r == c.end())
         {
             --r;
             break;
         }
         if(Cross(v.x - (r -> x), v.y - (r -> y), (now -> x) - (r -> x), (now -> y) - (r -> y)) <= )
         {
             --r;
             break;
         }
         sum -= Dis((now -> x), (now -> y), (r -> x), (r -> y));
         c.erase(now);
     }
     c.insert(v);
     sum += Dis((l -> x), (l -> y), v.x, v.y) + Dis(v.x, v.y, (r -> x), (r -> y));
 }
 int main()
 {
     o.x = o.y = ;
     c.insert(o);
     o.x = n = Get();
     c.insert(o);
     o.x = x = Get();
     o.y = y = Get();
     c.insert(o);
     m = Get();
     sum = Dis(, , x, y) + Dis(x, y, n, );
     for(int i = ; i <= m; ++i)
     {
         a[i].x = Get();
         a[i].y = Get();
     }
     e = Get();
     for(int i = ; i <= e; ++i)
     {
         flag[i] = Get();
         if(flag[i] == )
         {
             num[i] = Get();
             vis[num[i]] = true;
         }
     }
     for(int i = ; i <= m; ++i)
         if(!vis[i])
             Add(a[i]);
     for(int i = e; i >= ; --i)
     {
         if(flag[i] == ) Add(a[num[i]]);
         else ans[++nu] = sum;
     }
     for(int i = nu; i >= ; --i)
         printf("%.2lf\n", ans[i]);
 }