51Nod1766 树上的最远点对

1766 树上的最远点对

n个点被n-1条边连接成了一颗树，给出a_b和cd两个区间，表示点的标号请你求出两个区间内各选一点之间的最大距离，即你需要求出max｛dis(i,j) |a<=i<=b,c<=j<=d｝

（PS 建议使用读入优化）

输入

第一行一个数字 n n<=100000。

第二行到第n行每行三个数字描述路的情况， x,y,z (1<=x,y<=n,1<=z<=10000)表示x和y之间有一条长度为z的路。

第n+1行一个数字m，表示询问次数 m<=100000。

接下来m行，每行四个数a,b,c,d。

输出

共m行，表示每次询问的最远距离

输入样例

5

1 2 1

2 3 2

1 4 3

4 5 4

1

2 3 4 5

输出样例

10

题解

对于这个问题，我们不负责任的猜想一个性质。

对于l<k<r,编号在（l，r）之间的最远点对一定是编号在（l，k）的最远点对（a，b）和编号（k+1，r）的最远点对（c，d）四个端点组合成的六组点对：

（a，b）或（a，c）或（a，d）或（b，c）或（b，d）或（c，d）。

上述性质可以通过画图体会。

给一个不能再丑的图。

（画师：业界著名算法选手Claris）



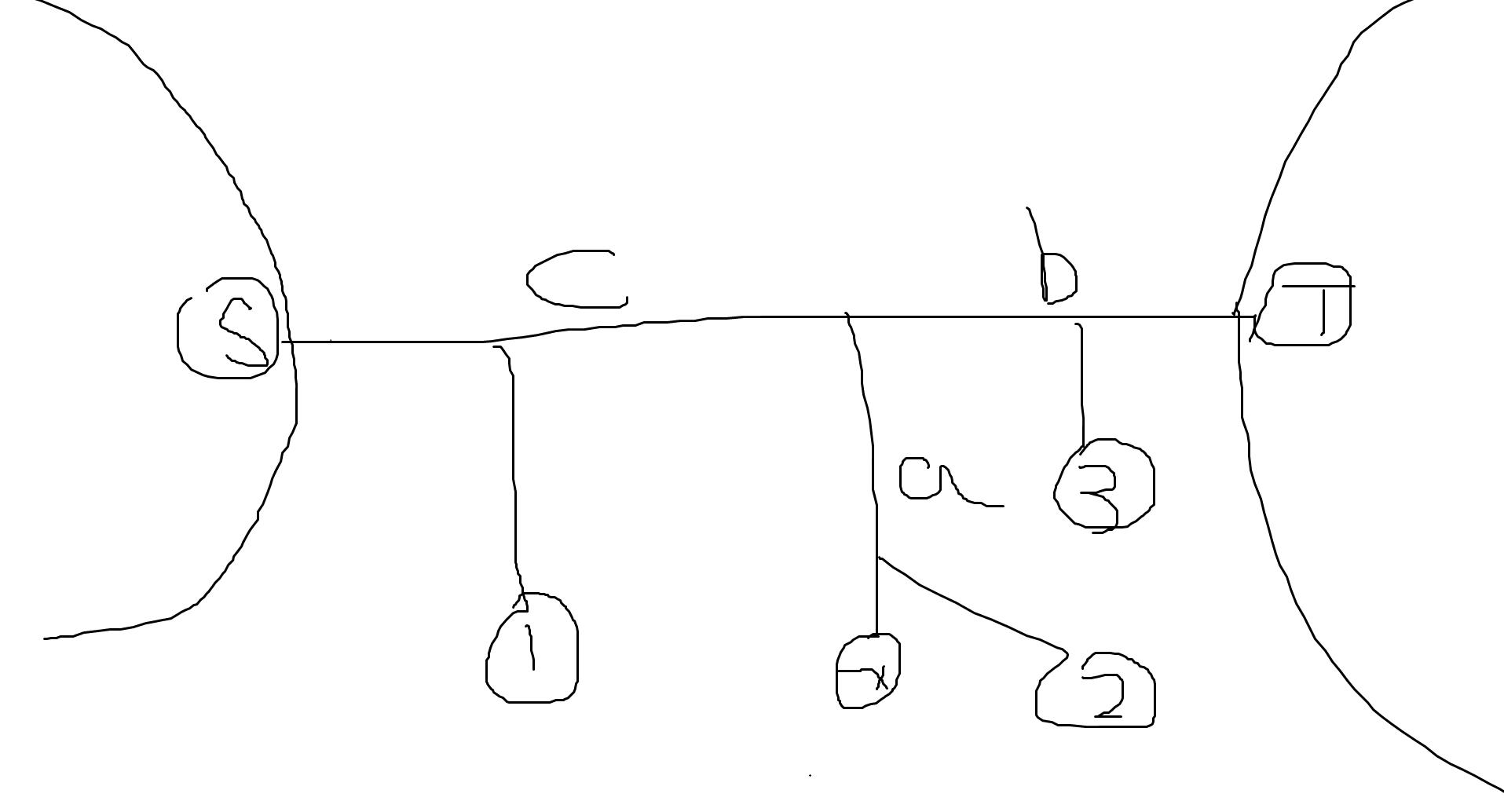
S和T是直径 x是另一个点 如果另一棵树的某个点 在S那个区域 那么因为a<=b 所以它走T就好了 然后这个点在T区域也是同理的 如果那个点是一号点 或者二号点也是同理 如果在3就可以走到S……然后这个过程是可以用线段树合并维护下的。

那么区间之间的最远点对就可以由两个它的子区间合并得到，可以使用线段树来维护O（nlogn）预处理，O(1)查询。

所以我们可以求出编号（a，b）之间的最远点对，编号（c，d）之间的最远点对，然后相互计算下距离即可。总复杂度O（nlogn）

这题除了结论有点意思（并且这官方题解里面也没哟证明！）之外，就没有什么意思了。

线段树+ST表.

树上最长链可以合并,只需要合并两个区间最长链的两个端点即可.

ST表要预处理好 log ,用了cmath 的 log2() ,T的飞起.

这样复杂度就是 O(nlogn)

#include<cstdio>
#include<cmath>
#include<cstring>
#include<utility>
#include<vector>
#include<iostream>
using namespace std;

#define debug(a) cout<<#a<<"="<<a<<" "
#define mpr make_pair
typedef pair< int,int > pr;
typedef long long LL;
const int N = 100050;
const int M = 25;

int n,m,cnt;
vector< pr > g[N];
int pow2[M],lg2[N<<1],dfs[N<<1],d[N],val[N],pos[N];
int f[N<<1][M];

inline int in(int x=0,char ch=getchar()){ while(ch>'9' || ch<'0') ch=getchar();
    while(ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x; }
void DFS(int u,int fa,int dep,int value){
    dfs[++m]=u,d[u]=dep,val[u]=value,pos[u]=m,f[m][0]=u;
    for(int i=0,v,lim=g[u].size();i<lim;i++) if((v=g[u][i].first)!=fa) DFS(v,u,dep+1,value+g[u][i].second),dfs[++m]=u,f[m][0]=u;
}
void init(){
    pow2[0]=1;for(int i=1;i<M;i++) pow2[i]=pow2[i-1]<<1;
    lg2[0]=-1;for(int i=1;i<=m;i++) lg2[i]=lg2[i>>1]+1;
    for(int j=1;j<M;j++) for(int i=1;i<=m;i++) if(i+pow2[j]-1<=m){
        int u=f[i][j-1],v=f[i+pow2[j-1]][j-1];
        if(d[u]<d[v]) f[i][j]=u;else f[i][j]=v;
    }
}
int Dis(int u,int v,int lca=0){
    if(pos[u]<pos[v]) swap(u,v);int lg=lg2[pos[u]-pos[v]+1];
    if(d[f[pos[v]][lg]]<d[f[pos[u]-pow2[lg]+1][lg]]) lca=f[pos[v]][lg];else lca=f[pos[u]-pow2[lg]+1][lg];
    return (LL)val[u]+val[v]-2*val[lca];
}
struct SegmentTree{
    #define lc (o<<1)
    #define rc (o<<1|1)
    #define mid ((l+r)>>1)
    #define Gd(u) Dis(u.first,u.second)
    pr g[N<<2];int d[N<<2];
    pr PushUp(pr u,pr v,int d1=0,int d2=0,int o=0){
        if(!d1 && !d2) d1=Gd(u),d2=Gd(v);
        pr res=d1>d2?u:v;int dd=max(d1,d2);
        if(Dis(u.first,v.first)>dd) res=mpr(u.first,v.first),dd=Gd(res);
        if(Dis(u.first,v.second)>dd) res=mpr(u.first,v.second),dd=Gd(res);
        if(Dis(u.second,v.first)>dd) res=mpr(u.second,v.first),dd=Gd(res);
        if(Dis(u.second,v.second)>dd) res=mpr(u.second,v.second),dd=Gd(res);
        if(o) d[o]=dd;return res;
    }
    void Build(int o,int l,int r){
        if(l==r){ g[o]=mpr(l,l),d[o]=0;return; }
        Build(lc,l,mid);Build(rc,mid+1,r);
        g[o]=PushUp(g[lc],g[rc],d[lc],d[rc],o);
    }
    pr Query(int o,int l,int r,int L,int R){
        if(L<=l && r<=R) return g[o];
        pr res=mpr(L,L);
        if(L<=mid) res=Query(lc,l,mid,L,R);
        if(R>mid) res=PushUp(res,Query(rc,mid+1,r,L,R));
        return res;
    }
    pr Merge(pr u,pr v){
        pr res=mpr(u.first,v.first);int d=Gd(res);
        if(Dis(u.first,v.second)>d) res=mpr(u.first,v.second),d=Gd(res);
        if(Dis(u.second,v.first)>d) res=mpr(u.second,v.first),d=Gd(res);
        if(Dis(u.second,v.second)>d) res=mpr(u.second,v.second),d=Gd(res);
        return res;
    }
    int Query(int a,int b,int c,int d){
        pr r1=Query(1,1,n,a,b),r2=Query(1,1,n,c,d),r3=Merge(r1,r2);
        return Gd(r3);
    }
    #undef lc
    #undef rc
    #undef mid
    #undef Gd
}seg;
int main(){
    n=in();memset(d,0x3f,sizeof(d));
    for(int i=1,u,v,w;i<n;i++) u=in(),v=in(),w=in(),g[u].push_back(mpr(v,w)),g[v].push_back(mpr(u,w));
    DFS(1,1,1,0),init(),seg.Build(1,1,n);
    for(int k=in(),a,b,c,d;k--;){
        a=in(),b=in(),c=in(),d=in();
        printf("%d\n",seg.Query(a,b,c,d));
    }return 0;
}