hdu6390 /// 欧拉函数+莫比乌斯反演 筛inv[] phi[] mu[]

题目大意：

给定m n p 求下式

 

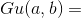
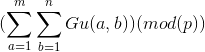
题解：https://blog.csdn.net/codeswarrior/article/details/81700226

莫比乌斯讲解：https://www.cnblogs.com/peng-ym/p/8647856.html

莫比乌斯的mu[]：https://www.cnblogs.com/cjyyb/p/7953803.html

#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define INF 0x3f3f3f3f
#define mem(i,j) memset(i,j,sizeof(i))
const int N=1e6+;

LL mu[N], phi[N];
LL inv[N];

int n,m,p;

void initinv() {
    inv[]=;
    for(int i=;i<N;i++)
        inv[i]=inv[p%i]*(LL)(p-p/i)%p;
} // 逆元
void init() {
    for(int i=;i<N;i++) phi[i]=i;
    for(int i=;i<N;i++)
        if(i==phi[i]) {
            for(int j=i;j<N;j+=i)
                phi[j]=phi[j]/i*(i-);
        }
    mem(mu,); mu[]=;
    for(int i=;i<N;i++)
        for(int j=i*;j<N;j+=i)
            mu[j]-=mu[i];
} // 欧拉 莫比乌斯

LL moblus(int a,int b,int g) {
    LL res=; a/=g,b/=g;
    /// gcd(1~a,1~b)=g -> gcd(1~a/g,1~b/g)=1
    for(int i=;i<=min(a,b);i++)
        res+=(LL)mu[i]*(a/i)*(b/i);
    /// mu[i] * (1~a,1~b)中[gcd=g或g的倍数]的数量
    return res;
}

int main()
{
    init();
    int t; scanf("%d",&t);
    while(t--) {
        scanf("%d%d%d",&m,&n,&p);
        LL ans=; initinv();
        for(int i=;i<=min(m,n);i++) {
            LL uF=moblus(n,m,i)%p;
            ans=(ans+uF*i%p*inv[phi[i]]%p)%p;
        }
        printf("%lld\n",ans);
    }

    return ;
}