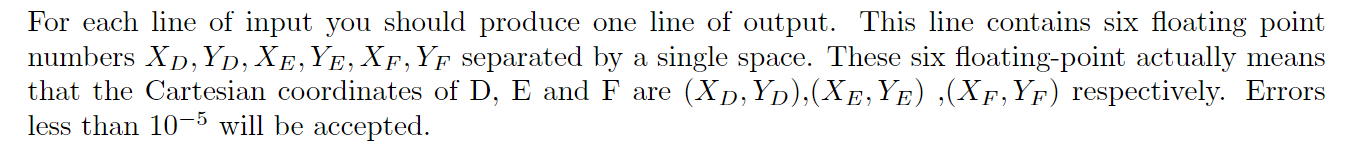UVA 11178 Morley's Theorem (坐标旋转)
题目链接:UVA 11178
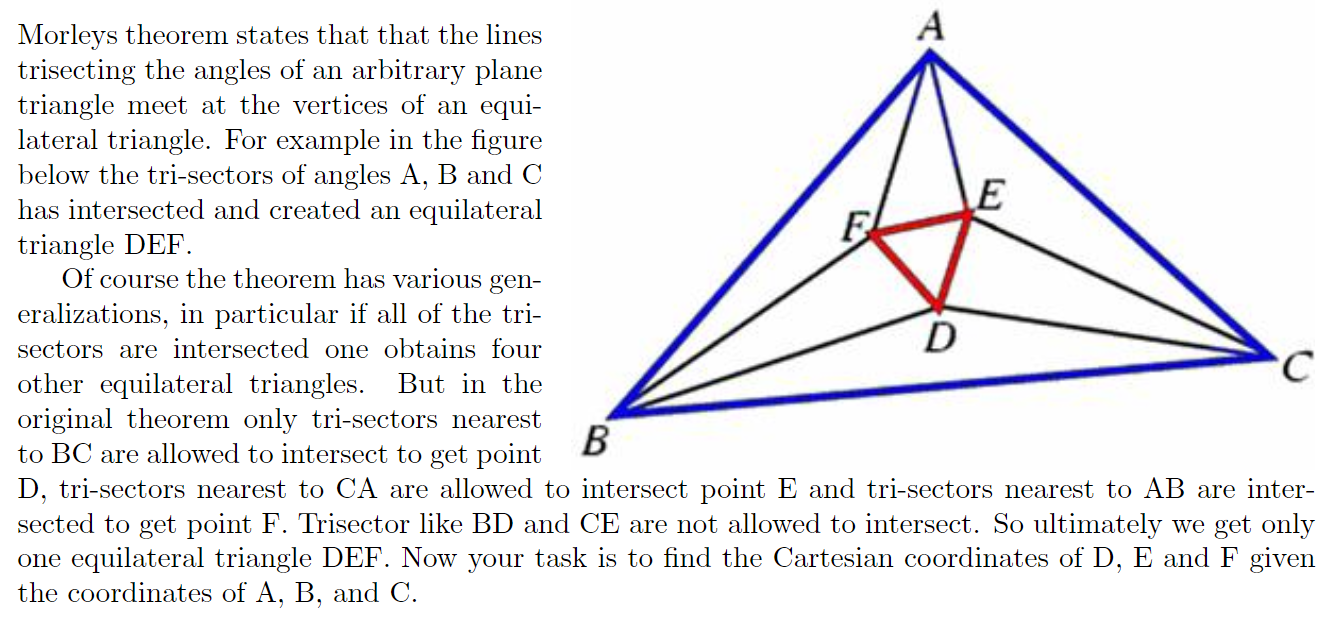
Description
Input
Output
Sample Input
Sample Output
Solution
题意
\(Morley's\ theorem\) 指任意三角形的每个内角的三等分线相交的三角形为等边三角形。
给出三角形的每个点的坐标,求根据 \(Morley's\ theorem\) 构造的等边三角形的三个点的坐标。
题解
对于点 \(D\),只需求直线 \(BC\) 绕点 \(B\) 旋转 \(\frac{1}{3} \angle ABC\) 的直线与直线 \(CB\) 绕点 \(C\) 旋转 \(\frac{1}{3} \angle ACB\) 的直线的交点。其他两点类似。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
const db eps = 1e-10;
const db pi = acos(-1.0);
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll maxn = 1e5 + 10;
inline int dcmp(db x) {
if(fabs(x) < eps) return 0;
return x > 0? 1: -1;
}
class Point {
public:
double x, y;
Point(double x = 0, double y = 0) : x(x), y(y) {}
void input() {
scanf("%lf%lf", &x, &y);
}
Point operator+(const Point a) {
return Point(x + a.x, y + a.y);
}
Point operator-(const Point a) {
return Point(x - a.x, y - a.y);
}
bool operator<(const Point &a) const {
return (!dcmp(y - a.y))? dcmp(x - a.x) < 0: y < a.y;
}
db dis2() {
return x * x + y * y;
}
db dis() {
return sqrt(dis2());
}
db dot(const Point a) {
return x * a.x + y * a.y;
}
db cross(const Point a) {
return x * a.y - y * a.x;
}
db ang(Point a) {
return acos(dot(a) / (a.dis() * dis()));
}
Point Rotate(double rad) {
return Point(x * cos(rad) - y * sin(rad), x * sin(rad) + y * cos(rad));
}
};
typedef Point Vector;
class Line {
public:
Point s, e;
db angle;
Line() {}
Line(Point s, Point e) : s(s), e(e) {}
inline void input() {
scanf("%lf%lf%lf%lf", &s.x, &s.y, &e.x, &e.y);
}
int toLeftTest(Point p) {
if((e - s).cross(p - s) > 0) return 1;
else if((e - s).cross(p - s) < 0) return -1;
return 0;
}
Point crosspoint(Line l) {
double a1 = (l.e - l.s).cross(s - l.s);
double a2 = (l.e - l.s).cross(e - l.s);
double x = (s.x * a2 - e.x * a1) / (a2 - a1);
double y = (s.y * a2 - e.y * a1) / (a2 - a1);
if(dcmp(x) == 0) x = 0;
if(dcmp(y) == 0) y = 0;
return Point(x, y);
}
};
Point get_crosspoint(Point A, Point B, Point C) {
Vector v1 = C - B;
db a1 = v1.ang(A - B);
v1 = v1.Rotate(a1 / 3.0);
v1 = v1 + B;
Vector v2 = B - C;
db a2 = v2.ang(A - C);
v2 = v2.Rotate(-a2 / 3.0);
v2 = v2 + C;
Line l1 = Line(B, v1);
Line l2 = Line(C, v2);
return l1.crosspoint(l2);
}
int main() {
int T;
scanf("%d", &T);
while(T--) {
Point a, b, c;
a.input(); b.input(); c.input();
Point d, e, f;
d = get_crosspoint(a, b, c);
e = get_crosspoint(b, c, a);
f = get_crosspoint(c, a, b);
printf("%.6lf %.6lf %.6lf %.6lf %.6lf %.6lf\n", d.x, d.y, e.x, e.y, f.x, f.y);
}
return 0;
}
UVA 11178 Morley's Theorem (坐标旋转)的更多相关文章
- Uva 11178 Morley's Theorem 向量旋转+求直线交点
http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=9 题意: Morlery定理是这样的:作三角形ABC每个 ...
- UVA 11178 Morley's Theorem(旋转+直线交点)
题目链接:http://acm.hust.edu.cn/vjudge/problem/viewProblem.action?id=18543 [思路] 旋转+直线交点 第一个计算几何题,照着书上代码打 ...
- uva 11178 - Morley's Theorem
http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&p ...
- UVA 11178 Morley's Theorem(几何)
Morley's Theorem [题目链接]Morley's Theorem [题目类型]几何 &题解: 蓝书P259 简单的几何模拟,但要熟练的应用模板,还有注意模板的适用范围和传参不要传 ...
- UVa 11178:Morley’s Theorem(两射线交点)
Problem DMorley’s TheoremInput: Standard Input Output: Standard Output Morley’s theorem states that ...
- UVA 11178 - Morley's Theorem 向量
http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&p ...
- 简单几何(求交点) UVA 11178 Morley's Theorem
题目传送门 题意:莫雷定理,求三个点的坐标 分析:训练指南P259,用到了求角度,向量旋转,求射线交点 /*********************************************** ...
- UVa 11178 Morley's Theorem (几何问题)
题意:给定三角形的三个点,让你求它每个角的三等分线所交的顶点. 析:根据自己的以前的数学知识,应该很容易想到思想,比如D点,就是应该求直线BD和CD的交点, 以前还得自己算,现在计算机帮你算,更方便, ...
- UVA 11178 Morley's Theorem 计算几何模板
题意:训练指南259页 #include <iostream> #include <cstdio> #include <cstring> #include < ...
随机推荐
- python pymouse用法记录
from pymouse import PyMouse m = PyMouse() m.position()#获取当前坐标的位置 m.move(x,y)#鼠标移动到xy位置 m.click(x,y)# ...
- Java第四次作业—面向对象高级特性(继承和多态)
Java第四次作业-面向对象高级特性(继承和多态) (一)学习总结 1.学习使用思维导图对Java面向对象编程的知识点(封装.继承和多态)进行总结. 2.阅读下面程序,分析是否能编译通过?如果不能,说 ...
- [已解决]报错: No module named pip
cmd中敲命令: python -m ensurepip 更新升级pip命令: python -m pip install --upgrade pip
- C#关键字扫盲——Tuple(元组类) 、ValueTuple(值元组)
原文:C#关键字扫盲--Tuple(元组类) .ValueTuple(值元组) 版权声明:本文为博主原创文章,随意转载. https://blog.csdn.net/Michel4Liu/articl ...
- 使用Hbuilder 报错The keyword 'export' is reserved
右击文件 > 验证本文档语法(V)后报错 解决: 项目右键->”属性”->”语法&框架”界面中配置项目的javaScript版本,将ECMAScript5.1 修改为6.
- postgresql like 中的转义
select * from tb_org where char_length(xdm)>8 and xdm not like '%*_%' ESCAPE '*' ESCAPE 后面的 * 是转 ...
- Ubuntu14.04.1LTS不能上网解决方法之一
我们在装好了Ubuntu之后,打开浏览器,显示Server not found. 1.点击网络图标,显示如下: 2.进入etc/NetworkManager,找到 Networkmanager.con ...
- 【JS学习】慕课网2-7 练习题:制作新按钮,“新窗口打开网站” ,点击打开新窗口。
要求: 1.新窗口打开时弹出确认框,是否打开 提示: 使用 if 判断确认框是否点击了确定,如点击弹出输入对话框,否则没有任何操作. 2.通过输入对话框,确定打开的网址,默认为 http://www. ...
- vue 使用Better-Scroll
注意点 1. 外层容器wrapper要设置高度,并且overflow:hidden. 2. wrapper里面的需要一个div包裹所有内容 3. 样式成功 4. 以上就是可以滚动的情况,wrappe ...
- mybatis xml中大于号小于号的代替
第一种写法(1): 原符号 < <= > >= & ' "替换符号 < <= > >= & ' " ...