poj 3744 矩阵快速幂+概率dp

题目大意：

输入n，代表一位童子兵要穿过一条路，路上有些地方放着n个地雷（1<=n<=10）。再输入p，代表这位童子兵非常好玩，走路一蹦一跳的。每次他在 i 位置有 p 的概率走一步到 i+1 ，或者 (1-p) 的概率跳一步到 i+2。输入n个数，代表n个地雷的位置（1<=n<=100000000），童子兵初始在1位置，求他安全通过这条道路的概率。

基本思路：

如果k 号位有雷，那么安全通过这个雷只可能是在 k-1 号位选择走两步到 k+1 号位。因此，可以得到如下结论：在第 i 个雷的被处理掉的概率就是从 a[i-1]+1 号位到 a[i] 号位的概率。于是，可以用 1 减去就可以求出安全通过第 i个雷的概率，最后乘起来即可，比较悲剧的是数据很大，所以需要用到矩阵快速幂……

类似斐波那契数列，有ans[i]=p*ans[i-1]+(1-p)*ans[i-2] ，构造矩阵为

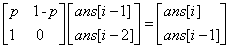
代码如下：

#include<cstdio>
#include<cstring>
#include<algorithm>
 
using namespace std;
 
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int maxn = 100000+10;
double f[3][3],base[3][3],tmp[3][3];
double b[3],c[3];
int n,pos[20];
double p;
double solve(int t){
 
    base[0][0]=p;
    base[0][1]=1.0-p;
    base[1][0]=1;
    base[1][1]=0;
    f[0][0]=1;
    f[0][1]=0;
    f[1][0]=0;
    f[1][1]=1;
    b[0]=1;
    b[1]=0;
    while(t){
        if(t&1){
            for(int i=0;i<2;i++){
                for(int j=0;j<2;j++){
                    tmp[i][j]=0;
                    for(int k=0;k<2;k++){
                        tmp[i][j]+=f[i][k]*base[k][j];
                    }
                }
            }
            for(int i=0;i<2;i++){
                for(int j=0;j<2;j++){
                    f[i][j]=tmp[i][j];
                }
            }
        }
        for(int i=0;i<2;i++){
            for(int j=0;j<2;j++){
                tmp[i][j]=0;
                for(int k=0;k<2;k++){
                    tmp[i][j]+=base[i][k]*base[k][j];
                }
            }
        }
        for(int i=0;i<2;i++){
            for(int j=0;j<2;j++){
                base[i][j]=tmp[i][j];
            }
        }
        t>>=1;
    }
    for(int i=0;i<2;i++){
        c[i]=0;
        for(int j=0;j<2;j++){
            c[i]+=f[i][j]*b[j];
        }
    }
    return c[0];
}
int main(){
    while(~scanf("%d%lf",&n,&p)){
        for(int i=1;i<=n;i++){
            scanf("%d",&pos[i]);
        }
        pos[0]=0;
        sort(pos,pos+n+1);
        double ans=1.0;
        for(int i=1;i<=n;i++){
            ans=ans*(1.0-solve(pos[i]-pos[i-1]-1));
        }
        printf("%.7lf\n",ans);
    }
    return 0;
}