POJ1741 Tree（树的点分治基础题）

Give a tree with n vertices,each edge has a length(positive integer less than 1001).
Define dist(u,v)=The min distance between node u and v. 
Give an integer k,for every pair (u,v) of vertices is called valid if and only if dist(u,v) not exceed k. 
Write a program that will count how many pairs which are valid for a given tree. 

Input

The input contains several test cases. The first line of each test case contains two integers n, k. (n<=10000) The following n-1 lines each contains three integers u,v,l, which means there is an edge between node u and v of length l. 
The last test case is followed by two zeros. 

Output

For each test case output the answer on a single line.

Sample Input

5 4
1 2 3
1 3 1
1 4 2
3 5 1
0 0

Sample Output

8

题意：

有一棵树，求满足x到y距离小于等于m的无序点对(x,y)的个数。

思路：

第一次写树上的乱搞系列。。。

对于此题，树上的分治。愚见如下。

假设有如图：

以root为根，点对(x,y)有四种情况。

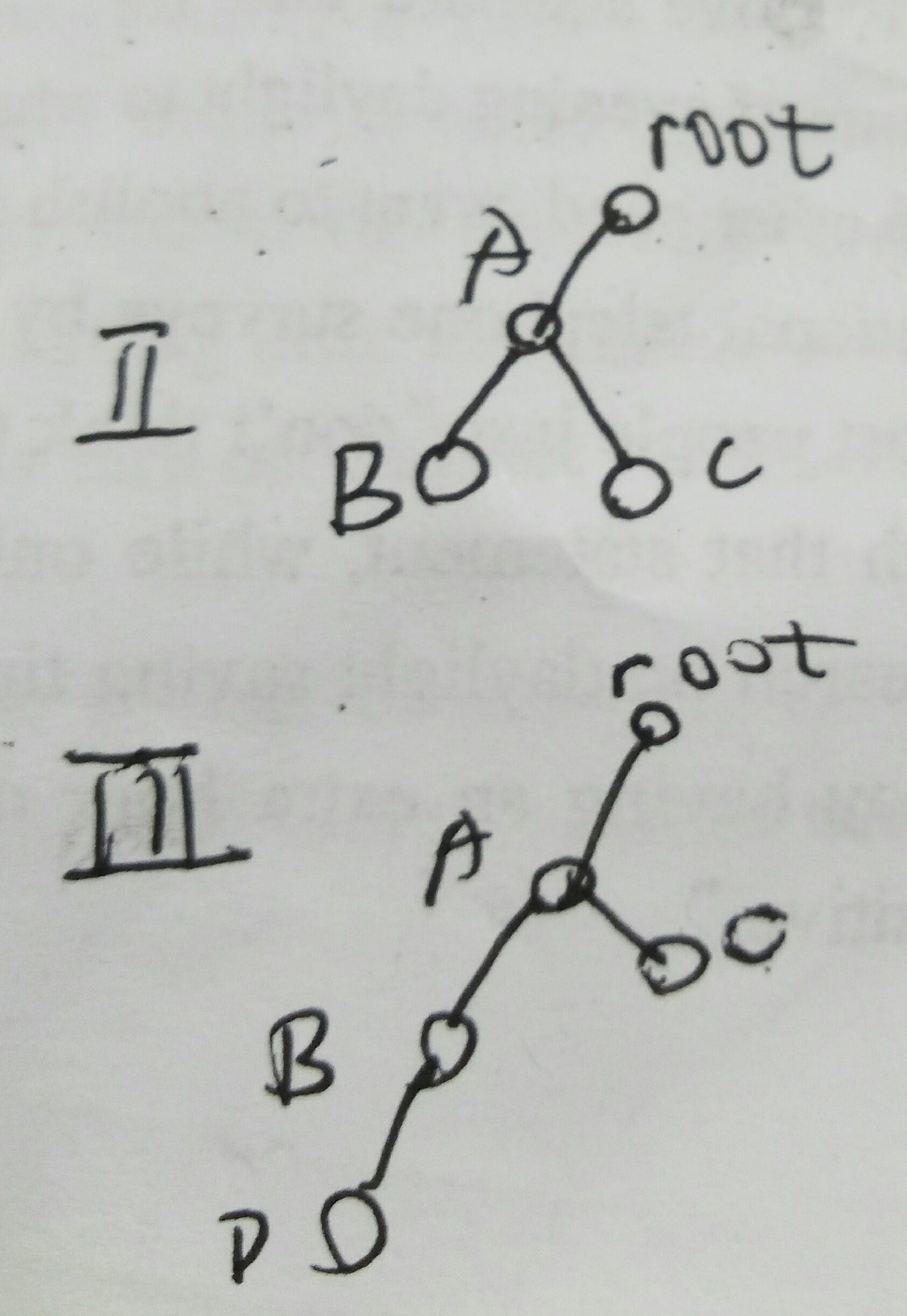
• 先说第四种，第四种是D-B-A-root-I..-X（经过root），dis(D,X)>m，无效，此处不考虑了。
• 第一种：A-root-I，经过root，而且dis(A,I)<=m，有效，累加。

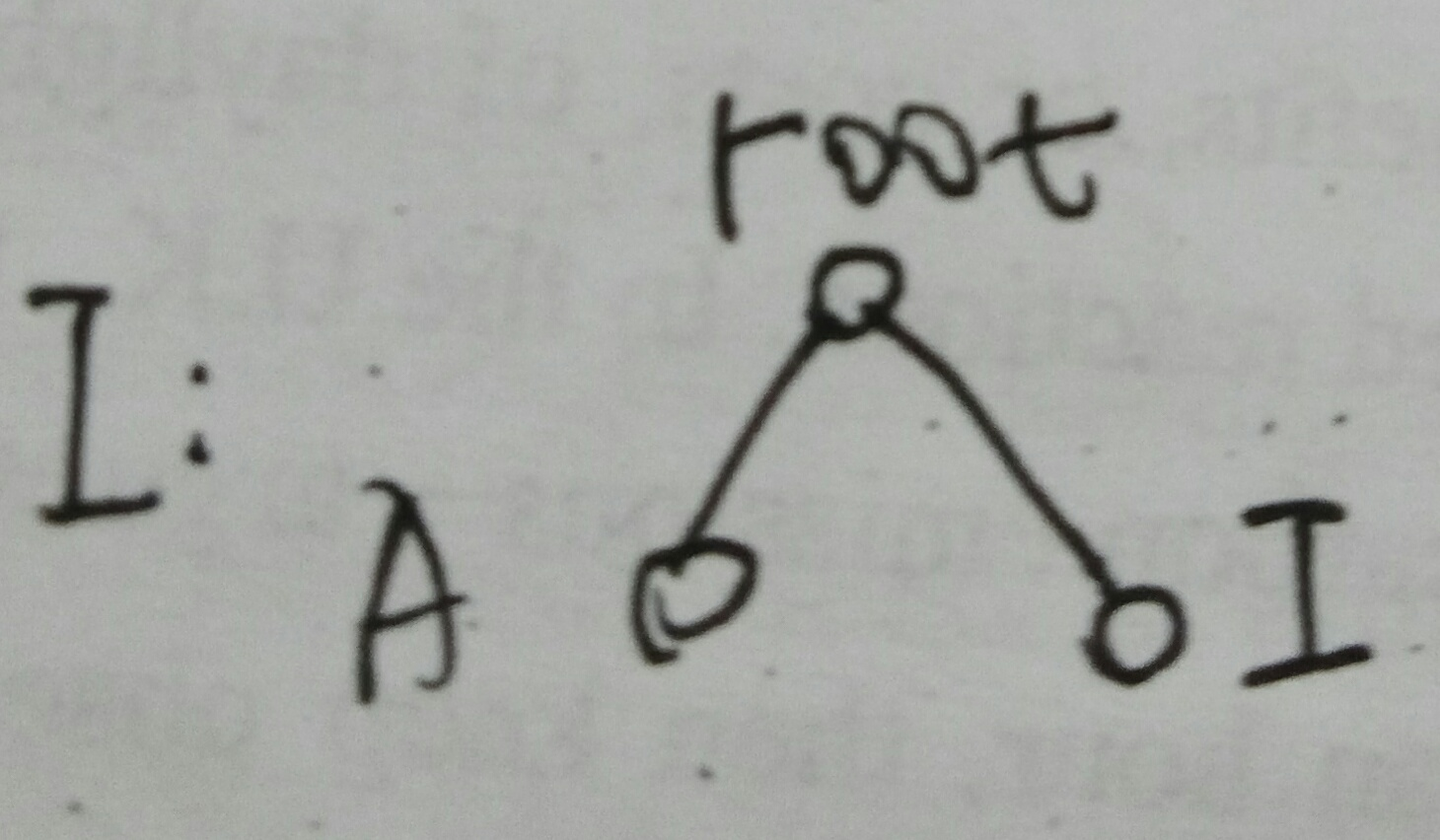
• 第二种：B-A-C,不经过root，但是dis(B,root)+dis(root,C)<=m，有效，累加。但是在当A为根时，点对(B,C)距离满足要求，肯定还会被算一次，所以此时需要减去儿子为根的某些部分。
• 第三种：D-B-A-C,不经过root，而且dis(D,root)+dis(root,C)>m,所以此处不累加。但是dis(B,A)+dis(A,C)<=m，当root下降到某点时会累加，这也是第二种需要减去的原因，防止累加两次。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 20010
using namespace std;
int m,head[N],to[N],len[N],next[N],cnt,sz[N];
int deep[N],root,vis[N],son[N],sn,d[N],tot,ans;
//son[]最大儿子树，sz[]子树。
//vis[]表示是否做为根使用过。
void add(int x,int y,int z)
{
    to[++cnt]=y,len[cnt]=z,next[cnt]=head[x],head[x]=cnt;
}
void getroot(int u,int fa)
{
    son[u]=,sz[u]=;
    for(int i=head[u];i;i=next[i])
      if(to[i]!=fa&&!vis[to[i]]){
        getroot(to[i],u);sz[u]+=sz[to[i]];
        son[u]=max(son[u],sz[to[i]]);
      }
    son[u]=max(son[u],sn-sz[u]);
    if(son[root]>son[u]) root=u;
}
void getdeep(int x,int fa)
{
    d[++tot]=deep[x];
    for(in
    t i=head[x];i;i=next[i])
      if(to[i]!=fa&&!vis[to[i]])
        deep[to[i]]=deep[x]+len[i],getdeep(to[i],x);
}
int calc(int x)
{
    tot=,getdeep(x,),sort(d+,d+tot+);
    int i=,j=tot,sum=;
    while(i<j) {                        //保证了不重复
        if(d[i]+d[j]<=m) sum+=j-i,i++ ; //d[]+d[]<m的个数。利用了双指针的思想
        else j--;
    }
    return sum;
}
void dfs(int u)
{
    deep[u]=;vis[u]=;ans+=calc(u);
    for(int i=head[u];i;i=next[i])
      if(!vis[to[i]]){
          deep[to[i]]=len[i];ans-=calc(to[i]);//居然是抽屉原理。。。 细思极恐
          sn=sz[to[i]];root=;getroot(to[i],);dfs(root);
      }
}
int main()
{
    int n,i,x,y,z;
    while(~scanf("%d%d",&n,&m)&&(n||m)){
        memset(head,,sizeof(head));
        memset(vis,,sizeof(vis));
        cnt=; ans=;
        for(i=;i<n;i++){
            scanf("%d%d%d",&x,&y,&z)
            add(x,y,z);add(y,x,z);
        }
        root=; son[]=0x7fffffff; sn=n;
        getroot(,); dfs(root);
        printf("%d\n",ans);
    }
    return ;
}