loj #2025. 「JLOI / SHOI2016」方

#2025. 「JLOI / SHOI2016」方

 

题目描述

上帝说，不要圆，要方，于是便有了这道题。

由于我们应该方，而且最好能够尽量方，所以上帝派我们来找正方形。上帝把我们派到了一个有 NNN 行 MMM 列的方格图上，图上一共有 (N+1)×(M+1)(N + 1) \times (M + 1)(N+1)×(M+1) 个格点，我们需要做的就是找出这些格点形成了多少个正方形（换句话说，正方形的四个顶点都是格点）。

但是这个问题对于我们来说太难了，因为点数太多了，所以上帝删掉了这 (N+1)×(M+1)(N + 1) \times (M + 1)(N+1)×(M+1) 中的 KKK 个点。既然点变少了，问题也就变简单了，那么这个时候这些格点组成了多少个正方形呢？

输入格式

第一行包含三个整数 NNN，MMM，KKK，代表棋盘的行数、列数和不能选取的顶点个数。 保证 N,M≤1N, M \leq 1N,M≤1，K≤(N+1)×(M+1)K \leq (N + 1) \times (M + 1)K≤(N+1)×(M+1)。
接下来 KKK 行，每行包含两个正整数 XXX，YYY，代表第 XXX 行第 YYY 列的格点被删掉了。保证 0≤X≤N,0≤Y≤M0 \leq X \leq N, 0 \leq Y \leq M0≤X≤N,0≤Y≤M，且不会出现重复的格点。约定每行的格点从上到下依次用整数 000 到 NNN 编号，每列的格点依次用 000 到 MMM 编号。

输出格式

输出一个正整数，代表正方形个数对 100000007100\,000\,007100000007（108+710^8 + 710​8​​+7）取模之后的数值。

样例

样例输入 1

2 2 4
1 0
1 2
0 1
2 1

样例输出 1

1

样例解释 1

如图所示，我们删掉了其中的四个格点，那么剩下的唯一的正方形便是最大的 2×22 \times 22×2 的正方形了。

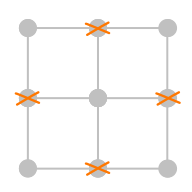
样例输入 2

7 10 5
2 3
1 5
6 2
3 5
2 6

样例输出 2

429

样例输入 3

2 2 4
0 0
2 2
0 2
2 0

样例输出 3

1

样例解释 3

还剩下一个边长为 2\sqrt 2√​2​​​ 的正方形。

数据范围与提示

Case #	N,MN, MN,M	KKK
1, 2	≤5\leq 5≤5	≤25\leq 25≤25
3, 4	≤50\leq 50≤50	≤50\leq 50≤50
5, 6	≤106\leq 10^6≤10​6​​	=0= 0=0
7, 8	≤106\leq 10^6≤10​6​​	≤50\leq 50≤50
9, 10	≤106\leq 10^6≤10​6​​	≤200\leq 200≤200
11, 12	≤103\leq 10^3≤10​3​​	≤2×103\leq 2 \times 10^3≤2×10​3​​
13 ~ 20	≤106\leq 10^6≤10​6​​	≤2×103\leq 2 \times 10^3≤2×10​3​​

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#define mod 100000007
#define maxn 2010
#define gets(x,y) (1LL*((x)+(y))*((y)-(x)+1)>>1)
using namespace std;
int n,m,cnt,ans,t1,t2,t3,t4,a[maxn],b[maxn];
struct node{
    int tot,fst[],px[maxn],py[maxn],nxt[maxn];
    void insert(int x,int y){
        int z=(x*+y)%;
        px[++tot]=x;py[tot]=y;
        nxt[tot]=fst[z];fst[z]=tot;
    }
    int find(int x,int y){
        int z=(x*+y)%;
        for(int p=fst[z];p;p=nxt[p])
            if(px[p]==x && py[p]==y)return ;
        return ;
    }
}hash;
bool inmp(int x,int y){return x>=&&x<=m&&y>=&&y<=n;}
void calc(int x,int y,int z){
    if(!x||!y||z<)return;
    z=min(z,x+y);
    x=min(x,z-);
    y=min(y,z-);
    t1=(t1+1LL*(z-y)*y)%mod;
    t1=(t1+gets(z-x,y-))%mod;
}
void update(int u1,int v1,int u2,int v2){
    if(inmp(u1,v1)&&inmp(u2,v2)){
        int tmp=hash.find(u1,v1)+hash.find(u2,v2);
        t2++;t3+=tmp;
        if(tmp>)t4++;
    }
}
void solve(int x1,int y1,int x2,int y2){
    int dx=x2-x1,dy=y2-y1;
    update(x1+dy,y1-dx,x2+dy,y2-dx);
    update(x1-dy,y1+dx,x2-dy,y2+dx);
    if(abs(dx+dy)&)return;
    dy=(dx+dy)>>;dx-=dy;
    update(x1+dx,y1+dy,x2-dx,y2-dy);
}
int main(){
    scanf("%d%d%d",&m,&n,&cnt);
    for(int i=;i<=cnt;i++){
        scanf("%d%d",&a[i],&b[i]);
        hash.insert(a[i],b[i]);
    }
    for(int i=;i<=m && i<=n;i++)
        ans=(ans+1LL*i*(m-i+)%mod*(n-i+))%mod;
    for(int i=;i<=cnt;i++){
        calc(a[i],m-a[i],b[i]);
        calc(a[i],m-a[i],n-b[i]);

        calc(b[i],n-b[i],a[i]);
        calc(b[i],n-b[i],m-a[i]);
        t1=(t1+min(a[i],b[i])+min(a[i],n-b[i])+min(m-a[i],b[i])+min(m-a[i],n-b[i]))%mod;
        for(int j=;j<i;j++)
            solve(a[i],b[i],a[j],b[j]);
    }
    printf("%d",(ans-t1+t2-t3/+t4/+mod)%mod);
    return ;
}