HDU 5251 矩形面积(二维凸包旋转卡壳最小矩形覆盖问题) --2015年百度之星程序设计大赛 - 初赛(1)
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define MAX 50010
using namespace std;
struct Point{
double x,y;
Point(double x=,double y=):x(x),y(y){}
};
Point P[MAX],ch[MAX];
typedef Point Vector;
typedef Point point;
Vector operator - (Point A,Point B)
{
return Vector(A.x-B.x,A.y-B.y);
}
bool operator <(const Point &a,const Point &b)
{
return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
const double eps=1e-;
int dcmp(double x)
{
if(fabs(x)<eps) return ; else return x<?-:;
}
bool operator ==(const Point &a,const Point &b)
{
return dcmp(a.x-b.x)==&&dcmp(a.y-b.y)==;
}
double Cross(Vector A,Vector B)
{
return A.x*B.y-A.y*B.x;
}
double dot(Vector A,Vector B)
{
return A.x*B.x+A.y*B.y;
}
int ConvexHull(Point *p,int n)
{
sort(p,p+n);
n=unique(p,p+n)-p;
int m=;
for(int i=;i<n;i++)
{
while(m>&&Cross(ch[m-]-ch[m-],p[i]-ch[m-])<=) m--;
ch[m++]=p[i];
}
int k=m;
for(int i=n-;i>=;i--)
{
while(m>k&&Cross(ch[m-]-ch[m-],p[i]-ch[m-])<=) m--;
ch[m++]=p[i];
}
if(n>) m--;
return m;
}
double Length(Vector A)
{
return dot(A,A);
}
double rotating_calipers(Point *p,int n)
{
int l=,r=,w;
double ans=1e30;
p[n]=p[];
for(int i=;i<n;i++)
{
//注意这里等于0一定要算上
//这里debug了整整一个小时 - -|||||
//找到至高点
while(dcmp(Cross(p[i+]-p[i],p[w+]-p[i])-Cross(p[i+]-p[i],p[w]-p[i]))>=) //因为边平行的时候面积相等 虽然如此但还是要继续找下一个 横着爬不动的意思
w=(w+)%n;
//找到最右的点 不可能向左的
while(dcmp(dot(p[i+]-p[i],p[r+]-p[i])-dot(p[i+]-p[i],p[r]-p[i]))>) //凸包不可能凹进去 所以不需要等号 加深对凸包求解过程的理解
r=(r+)%n;
if(i==) l=r;
while(dcmp(dot(p[i+]-p[i],p[l+]-p[i])-dot(p[i+]-p[i],p[l]-p[i]))<=) //必须加等号 否则凸包遇到直边的时候拐不过来 上不去 第二组样例可以完美说明问题
l=(l+)%n;
double d=Length(p[i+]-p[i]);
double area=fabs(Cross(p[i+]-p[i],p[w]-p[i]))
*fabs(dot(p[i+]-p[i],p[r]-p[i])-dot(p[i+]-p[i],p[l]-p[i]))/d;
//cout<<fabs(Cross(p[i+1]-p[i],p[w]-p[i]))<<" "; 这里灵活运用点积求底边长度 上面那一整行化简后就是底边长度
//cout<<"rrrrr "<<r<<" lll "<<l<<endl;
//cout<<dot(p[i+1]-p[i],p[r]-p[i])<<" "<<dot(p[i+1]-p[i],p[l]-p[i])<<endl;
ans=min(ans,area);
}
return ans;
}
int main()
{
int t,n,cas=;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
n*=;
for(int i=;i<n;i++)
scanf("%lf%lf",&P[i].x,&P[i].y);
int m=ConvexHull(P,n);
//for(int i=0;i<n;i++)
//cout<<ch[i].x<<" "<<ch[i].y<<endl;
double ans;
if(m<) ans=;
else ans=rotating_calipers(ch,m);
long long tmp = ans+0.5;
printf("Case #%d:\n%lld\n",cas++,tmp);
}
return ;
}
分析过程:
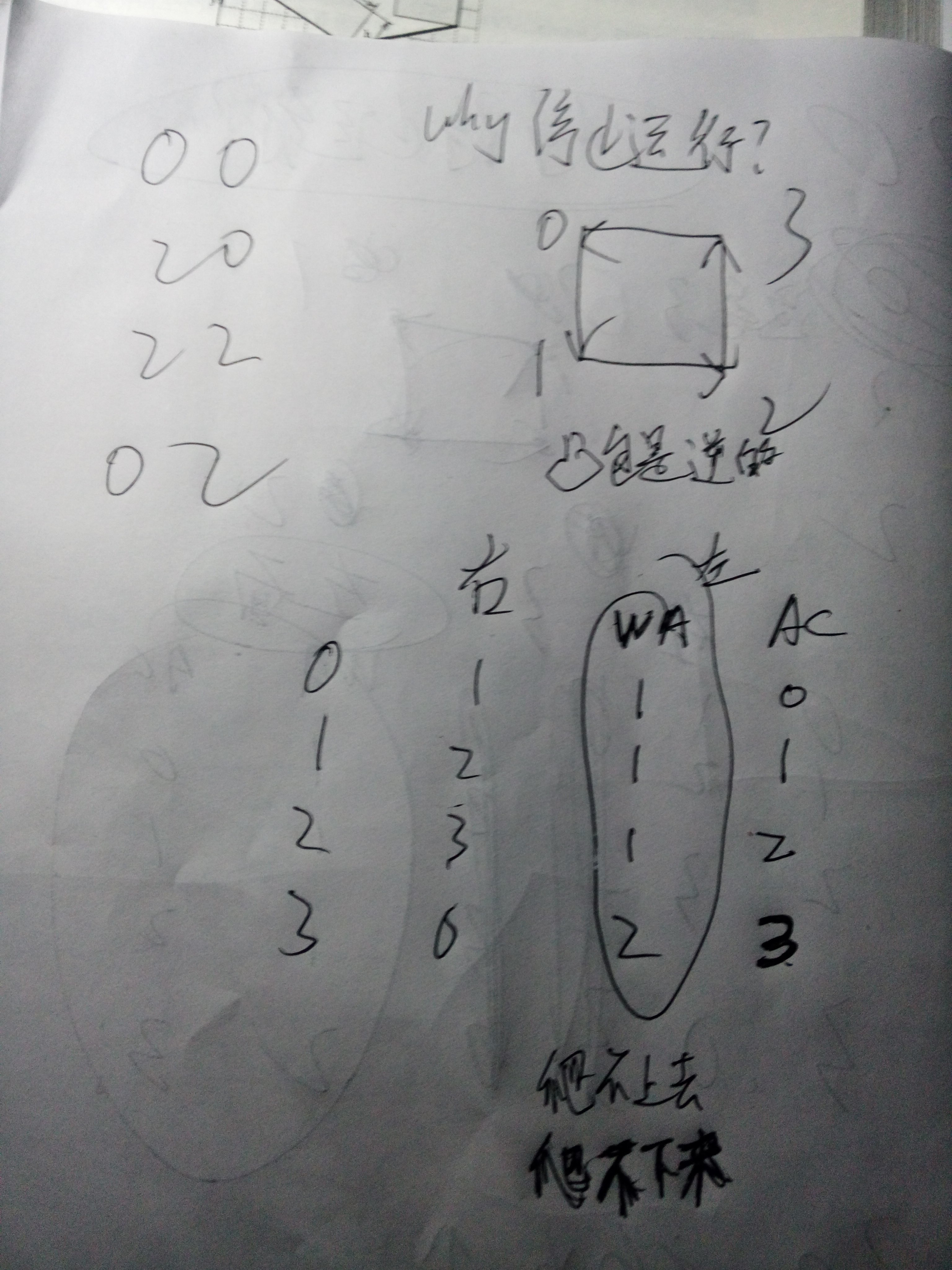
HDU 5251 矩形面积(二维凸包旋转卡壳最小矩形覆盖问题) --2015年百度之星程序设计大赛 - 初赛(1)的更多相关文章
- hdu 5253 连接的管道(kruskal)(2015年百度之星程序设计大赛 - 初赛(2))
连接的管道 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Subm ...
- poj 2079 Triangle (二维凸包旋转卡壳)
Triangle Time Limit: 3000MS Memory Limit: 30000KB 64bit IO Format: %I64d & %I64u Submit Stat ...
- poj 2187 Beauty Contest(二维凸包旋转卡壳)
D - Beauty Contest Time Limit:3000MS Memory Limit:65536KB 64bit IO Format:%I64d & %I64u ...
- HDU 6119 小小粉丝度度熊 【预处理+尺取法】(2017"百度之星"程序设计大赛 - 初赛(B))
小小粉丝度度熊 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Sub ...
- HDU 6114 Chess 【组合数】(2017"百度之星"程序设计大赛 - 初赛(B))
Chess Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submi ...
- 2019 年百度之星·程序设计大赛 - 初赛一 C. HDU 6670 Mindis 离散化+dijkstra
题目链接 :http://acm.hdu.edu.cn/showproblem.php?pid=6670 Mindis Time Limit: 4000/2000 MS (Java/Others) M ...
- HDU 6118 度度熊的交易计划 【最小费用最大流】 (2017"百度之星"程序设计大赛 - 初赛(B))
度度熊的交易计划 Time Limit: 12000/6000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total S ...
- HDU 6109 数据分割 【并查集+set】 (2017"百度之星"程序设计大赛 - 初赛(A))
数据分割 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submis ...
- HDU 6108 小C的倍数问题 【数学】 (2017"百度之星"程序设计大赛 - 初赛(A))
小C的倍数问题 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Sub ...
随机推荐
- Hive的数据库和表
本文介绍一下Hive中的数据库(Database/Schema)和表(Table)的基础知识,由于篇幅原因,这里只是一些常用的.基础的. Hive的数据库和表 先看一张草图: Hive结构 从图上可以 ...
- 【转载】java 客户端链接不上redis解决方案 (jedis)
本文出自:http://blog.csdn.net/lulidaitian/article/details/51946169 出现问题描述: 1.Could not get a resource fr ...
- python学习之数据类型与运算符号
python版本:3.6 python编辑器:pycharm 最新版本 整理成代码如下: #!/usr/bin/env python #-*- coding: utf-8 -*- # 数学操作符 pr ...
- 学习python第十四天,模块
Python 模块(Module),是一个 Python 文件,以 .py 结尾,包含了 Python 对象定义和Python语句. 模块让你能够有逻辑地组织你的 Python 代码段. 把相关的代码 ...
- 搭建一个简单的dns缓存服务器
环境:linux 软件:bind97,bind97-utils, bind97-libs ip:192.168.192.130:192.168.192.131 -------------------- ...
- 适合pc端的移动拖拽,分享一下。
h5新加的特性拖拽事件,但是只适合PC端哦.不多说了上代码 <!DOCTYPE html> <html> <head> <title></titl ...
- spark&dataframe
1.今天,我们来介绍spark以及dataframe的相关的知识点,但是在此之前先说一下对以前的hadoop的一些理解 当我启动hadoop的时候,上面有hdfs的存储结构,由于这个是分布式存储,所以 ...
- Javascript Step by Step - 02
DOM 操作 DOM是面向HTML和XML文档的API,为文档提供了结构化表示.在DOM中一切都是节点Node,文档就是由许多的Node组成的.文档里的每个节点都有属性 nodeName.nodeVa ...
- loj2100 「TJOI2015」线性代数
先推公式,推出个这,然后因为是 \(0/1\) 矩阵,选一个有损耗,两个一组有加成,就想到了最大权闭合子图,(飞行计划问题) #include <iostream> #include &l ...
- JavaScript - 问题集 - 含function的json对象与json字符串之间相互转换
基本的转换为:JSON.parse与JSON.stringify. 但是json数据中含function,则转换后,function会丢失,如: var json={ test:'test', log ...
