（转）Gamma分布，Beta分布，Multinomial多项式分布，Dirichlet狄利克雷分布

1. Gamma函数

首先我们可以看一下Gamma函数的定义：

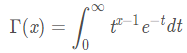
Gamma的重要性质包括下面几条：

1. 递推公式：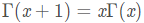

2. 对于正整数n, 有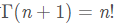

因此可以说Gamma函数是阶乘的推广。

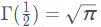
关于递推公式，可以用分部积分完成证明：

2. Beta函数

B函数，又称为Beta函数或者第一类欧拉积分，是一个特殊的函数，定义如下：

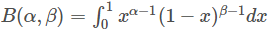
B函数具有如下性质：

3. Beta分布

在介绍贝塔分布(Beta distribution)之前，需要先明确一下先验概率、后验概率、似然函数以及共轭分布的概念。

1. 通俗的讲，先验概率就是事情尚未发生前，我们对该事发生概率的估计。利用过去历史资料计算得到的先验概率，称为客观先验概率；当历史资料无从取得或资料不完全时，凭人们的主观经验来判断而得到的先验概率，称为主观先验概率。例如抛一枚硬币头向上的概率为0.5，这就是主观先验概率。
2. 后验概率是指通过调查或其它方式获取新的附加信息，利用贝叶斯公式对先验概率进行修正，而后得到的概率。
3. 先验概率和后验概率的区别：先验概率不是根据有关自然状态的全部资料测定的，而只是利用现有的材料(主要是历史资料)计算的；后验概率使用了有关自然状态更加全面的资料，既有先验概率资料，也有补充资料。另外一种表述：先验概率是在缺乏某个事实的情况下描述一个变量；而后验概率（Probability of outcomes of an experiment after it has been performed and a certain event has occured.）是在考虑了一个事实之后的条件概率。
4. 共轭分布(conjugacy)：后验概率分布函数与先验概率分布函数具有相同形式。

先验概率和后验概率的关系为：

Beta分布的概率密度函数为：

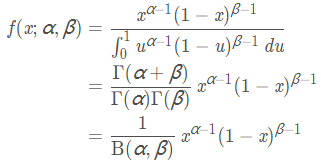
随机变量X服从参数为 α , β的Β分布通常写作：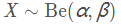

Beta分布与Gamma分布的关系为：

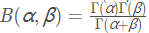
在beta分布中，B函数是一个标准化函数，它只是为了使得这个分布的概率密度积分等于1才加上的。后面狄利克雷的B函数也是一样的目的。

用一句话来说，beta分布可以看作一个概率的概率分布，当你不知道一个东西的具体概率是多少时，它可以给出了所有概率出现的可能性大小。

Beta分布的期望与方差分别为：

4. Beta分布是二项分布的共轭先验

这个结论很重要，在实际中应用也相当广泛。
在这之前，我们先简单回顾一下伯努利分布与二项分布。
伯努利分布(Bernoulli distribution)有称为0-1分布，伯努利分布式基于伯努利实验(Bernoulli trial)而来。

伯努利试验是只有两种可能结果的单次随机试验,即对于一个随机变量X来说:

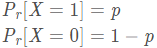
伯努利实验本质上即为"YES OR NO"的问题。最常见的一个例子就是抛硬币。
如果进行一次伯努利实验，假设成功(X=1)的概率为p (0 <= p <= 1)，失败(X=0)的概率为1−p，称随机变量X服从伯努利分布。

二项分布(Binomial distribution)是n重伯努利试验成功次数的离散概率分布。
如果试验E是一个n重伯努利试验，每次伯努利试验的成功概率为p，X代表成功的次数，则X的概率分布是二项分布，记为X~B(n,p)，其概率质量函数为:

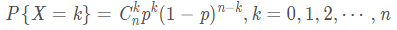
从上面的定义很明显可以看出，伯努利分布是二项分布在n=1时的特例。
二项分布使用最广泛的例子就是抛硬币了，假设硬币正面朝上的概率为p，重复扔n次硬币，k次为正面的概率即为一个二项分布概率。

在实验数据较少的情况下，如果我们直接用极大似然估计，二项分布的参数可能会出现过拟合的现象。比如，扔硬币三次都是正面，那么最大似然法预测以后的所有抛硬币结果都是正面。为了避免这种情况的发生，可以考虑引入先验概率分布p(μ)来控制参数μ，防止过拟合现象的发生。那么我们应该如何选择p(μ)？

前面我们提到，先验概率和后验概率的关系为：

二项分布的似然函数为: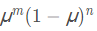

如果选择的先验概率p(μ)也是μ与(1−μ)次方乘积的关系，那么后验概率的分布形式与先验将一样，这样先验概率与后验概率就是共轭分布了。

由第三部分，我们知道Beta分布的概率密度函数为：

正好满足我们上面的要求！所以说，Beta分布式二项式分布的共轭先验！

5. Multinomial多项式分布

将二项式分布推广到多项式分布(Multinomial Distribution)，二项式分布式n次伯努利实验，规定了每次的实验结果只有两个。现在还是做n次实验，只不过每次实验的结果变成了m个，且m个结果发生的概率互斥且和为1，则发生其中一个结果X次的概率就是多项式分布。
扔骰子是典型的多项式分布。骰子有6个面对应6个不同的点数，这样单次每个点数朝上的概率都是1/6（对应p1~p6，它们的值不一定都是1/6，只要和为1且互斥即可，比如一个形状不规则的骰子）,重复扔n次，如果问有k次都是点数6朝上的概率就是：

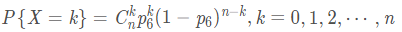
而多项式分布的一般概率质量函数为：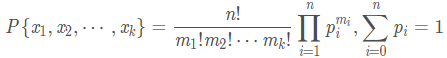

将试验进行N次，记第i种可能发生的次数为mi，其中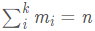

简单推导一下概率质量函数的推导：
k种独立的取值可能，n次实验，每种可能的概率为p1, p2, ..., pk。
则第一种被选中m1次，第二种被选中m2次，第k种被选中mk次的概率为：

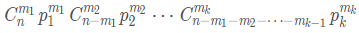
展开既可以得到上面的结果。

6. Dirichlet狄利克雷分布

前面我们讲到Beta分布式二项式分布的共轭先验，Dirichlet分布则是多项式分布的共轭先验。
Dirichlet（狄利克雷）同时可以看做是将Beta分布推广到多变量的情形。概率密度函数定义如下：

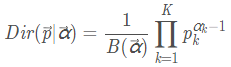
其中

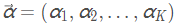
为Dirichlet分布的参数。且有：

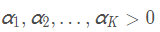
B(α)表示 Dirichlet分布的归一化常数：

类似于Beta函数有以下等式成立：

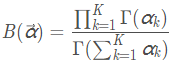
Dirichlet分布的期望为：

7. Dirichlet分布是Multinomial分布的共轭先验

多项式分布的似然函数为:

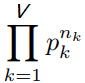
我们使用贝叶斯定理推断Dirichlet-MultCount共轭关系。对于参数为α的Dirichlet分布，可以用如下公式表示：

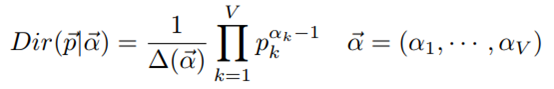
这里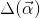，表达式如下：

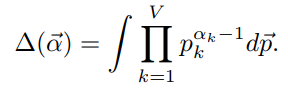
进行了多项式分布实验后，得到结果n后，后验分布为：

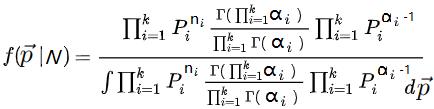
然后后验分布其实是一个新的狄利克雷分布：

参数n与α确定后，后验分布的期望为：

https://blog.csdn.net/bitcarmanlee/article/details/82156281#commentBox

https://www.cnblogs.com/coshaho/p/9740168.html

https://zhuanlan.zhihu.com/p/85220507