[POJ 1410] Intersection（线段与矩形交）

题目链接：http://poj.org/problem?id=1410

Intersection

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 12822		Accepted: 3347

Description

You are to write a program that has to decide whether a given line segment intersects a given rectangle.

An example: 
line: start point: (4,9) 
end point: (11,2) 
rectangle: left-top: (1,5) 
right-bottom: (7,1)

 
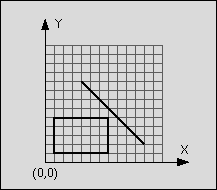
Figure 1: Line segment does not intersect rectangle

The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.

Input

The input consists of n test cases. The first line of the input file contains the number n. Each following line contains one test case of the format: 
xstart ystart xend yend xleft ytop xright ybottom

where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.

Output

For each test case in the input file, the output file should contain a line consisting either of the letter "T" if the line segment intersects the rectangle or the letter "F" if the line segment does not intersect the rectangle.

Sample Input

1
4 9 11 2 1 5 7 1

Sample Output

F

解题思路：

题意很清楚，就是判断一个线段是否和矩形相交。而所谓“相交”，但是这个相交的定义是线段在矩形内或者线段与矩形的边相交。

判断方法：

判断线段的两端点是否在矩形内，若是，则线段在矩形内。

判断线段是否与矩形相交，即是否和矩形的四条边中的任意一条边相交（规范相交和不规范相交都算）。

其实这是一个很好的模板题，注意处理下就可以了！

ACcode：

#include<iostream>
#include<stdio.h>
#include<string>
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<string.h>
#include<stdlib.h>
#include<math.h>
#include<algorithm>
#define PI 3.1415926
#define MOD 10000000007
#define N 1000005
#define INF 0x7fffffff
using namespace std;
typedef long long LL;
const double eps=1e-;
//点
struct point
{
    double x,y;
};
//线段
struct line
{
    point p1,p2;
} l;
//面
struct poly
{
    int n;//几个面
    double area;
    point plist[];
} rec;
//点乘
double dotdel(double x1,double y1,double x2,double y2)
{
    return x1*x2+y1*y2;
}
//叉乘
double crossmul(double x1,double y1,double x2,double y2)
{
    return x1*y2-x2*y1;
}
//判断是否为0，达到一定精度即认为成立
int cmpzero(double d)
{
    return (fabs(d)<eps)?:(d>?:-);
}
//右手螺旋定则，1:a在cd右侧，-1:a在cd左侧，0:三点共线
int cross(point a,point c,point d)
{
    return cmpzero(crossmul(a.x-c.x,a.y-c.y,d.x-c.x,d.y-c.y));
}
//在cross(a,c,d)==0的基础上，可判断点a是否在cd内部
int between(point a,point c,point d)
{
    return cmpzero(dotdel(c.x-a.x,c.y-a.y,d.x-a.x,d.y-a.y))!=;
}
//两线段相交情况：0:不相交，1:规范相交，2:不规范相交（交于端点或重合）
int seg_intersect(point a,point b,point c,point d)
{
    int a_cd=cross(a,c,d);
    if(a_cd== && between(a,c,d))
        return ;
    int b_cd=cross(b,c,d);
    if(a_cd== && between(a,c,d))
        return ;
    int c_ab = cross(c, a, b);
    if (c_ab ==  && between(c, a, b))
        return ;
    int d_ab=cross(d,a,b);
    if(d_ab== && between(d,a,b))
        return ;
    if((a_cd^b_cd)==- && (c_ab^d_ab)==-)
        return ;
    return ;
}
//使用有向面积法判断点是否在多边形内
bool point_in_poly(point p)
{
    double s=0.0;
    for(int i=; i<rec.n; i++)
        s+=fabs(crossmul(rec.plist[i].x-p.x,rec.plist[i].y-p.y,rec.plist[(i+)%rec.n].x-p.x,
                         rec.plist[(i+)%rec.n].y-p.y));
    if(cmpzero(s-rec.area)==) return true;
    else return false;
}
//判断线段是否与多边形相交
bool rec_seg_intersect()
{
    if(point_in_poly(l.p1) && point_in_poly(l.p2))
        return ;
    else if(seg_intersect(l.p1,l.p2,rec.plist[],rec.plist[])
            || seg_intersect(l.p1,l.p2,rec.plist[],rec.plist[])
            || seg_intersect(l.p1,l.p2,rec.plist[],rec.plist[])
            || seg_intersect(l.p1,l.p2,rec.plist[],rec.plist[]))
        return ;
    return ;
}
//计算多边形面积
void getarea()
{
    double s=rec.plist[].y*(rec.plist[rec.n-].x-rec.plist[].x);
    for(int i=; i<rec.n; i++)
        s+=rec.plist[i].y*(rec.plist[i-].x-rec.plist[(i+)%rec.n].x);
    rec.area=s;
}
int main()
{
    int T;
    double x1,y1,x2,y2,t;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%lf%lf%lf%lf",&l.p1.x,&l.p1.y,&l.p2.x,&l.p2.y);
        scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
        if(x1>x2)
        {
            t=x1;
            x1=x2;
            x2=t;
        }
        if(y2>y1)
        {
            t=y1;
            y1=y2;
            y2=t;
        }
        rec.n=;
        rec.plist[].x=x1;
        rec.plist[].y=y1;
        rec.plist[].x=x1;
        rec.plist[].y=y2;
        rec.plist[].x=x2;
        rec.plist[].y=y2;
        rec.plist[].x=x2;
        rec.plist[].y=y1;
        getarea();
        puts(rec_seg_intersect()?"T":"F");
    }
    return ;
}