Leetcode题解（十）

29、Divide Two Integers

题目

题目要求不用乘除和取模运算，实现两个整数相除；

我的第一想法就是把除法变成减法来做，这也是最初除法的定义，其实现代码如下：

 class Solution {
 public:
     int divide(int dividend, int divisor) {
         if( == divisor)
             return dividend;
         if (- == divisor)
             return -dividend;

         bool flag = false;

         if((dividend<&&divisor>))
         {
             dividend = -dividend;
             flag = true;
         }
         else if(dividend>&&divisor<)
         {
             divisor = -divisor;
             flag = true;
         }

         dividend = abs(dividend);
         divisor = abs(divisor);

         int result = ;
         while (dividend >=divisor)
         {
             dividend -= divisor;
             result++;
         }
         if(flag)
             result =  - result;

         return result;

     }
 };

看似没什么问题，但是其效率是不高的，比如被除数很大，而除数很小的时候，while循环会执行很多次，导致其效率不高，因此需要想想其他的办法解决该问题；既然直接做减法会超时，那姑且只能想移位操作了，因为移位操作是比较高效的操作，能够快速得到想要结果。如果是移位操作，应该如何下手呢？任何一个整数可以表示成以2的幂为底的一组基的线性组合，即num=a_0*2^0+a_1*2^1+a_2*2^2+...+a_n*2^n，在做除法时，dividend/divisor = num，变换一下就可以写成这样dividend = divisor*（a_0*2^0+a_1*2^1+a_2*2^2+...+a_n*2^n）；因此先让divisor左移n位，然后用dividend减去这个数，剩下的结果继续用同样的方法求解n-1，代码如下：

 class Solution {
 public:
    int divide(int dividend, int divisor) {
         // Note: The Solution object is instantiated only once.
         long long a = abs((double)dividend);
         long long b = abs((double)divisor);
         long long res = ;
         while(a >= b)
         {
             long long c = b;
             for(int i = ; a >= c; i++, c <<=)
             {
                 a -= c;
                 res += <<i;
             }
         }

         if((dividend ^ divisor) >> )
             res = -res;
         if(res >= )
             return ;
         else
             return res;

     }
 };

---------------------------------------------------------------------------------------------分割线--------------------------------------------------------------------------------

30、Substring with Concatenation of All Words

题目：

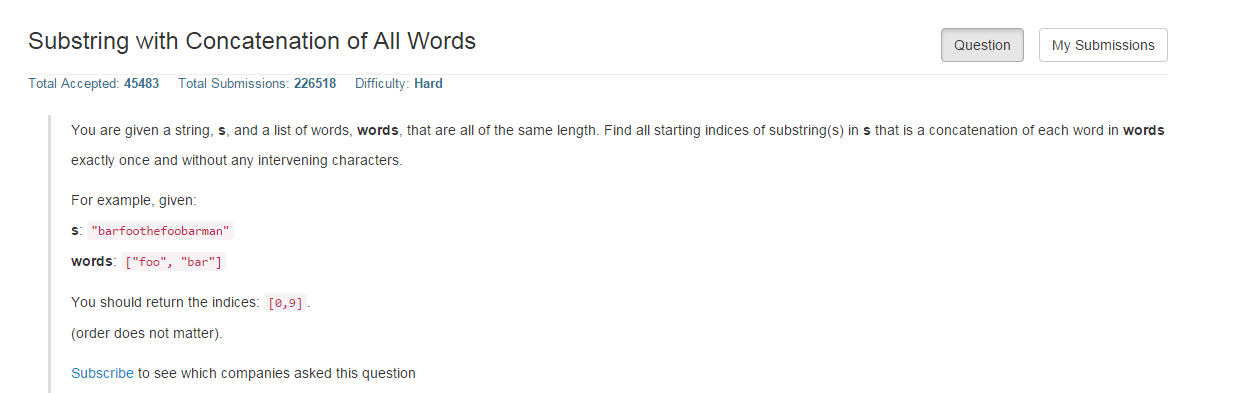
首先得弄懂题目的意思，这道题看了很久才弄明白题目意思：也就是说，给定一个字符串数组，数组中的字符串不管以什么顺序拼接在一起，得到新的字符串new，然后在s中查找new在s中第一次出现的下标，题目给的例子可以拼接成foobar或者barfoo，然后判断其起始下标分别为9,0；

按照上面说的，可以做n!次拼接，然后通过kmp算法判断在s中出现的下标，但是这种方式的效率太低，得想想其他方法，降低算法时间复杂度；

想了一会，想到了一个解决该问题的方法：依次遍历字符串s，第i（i从0开始）轮遍历时，也就是从s的s[i]开始，依次截取子字符串，截取长度为一个word的长度，然后判断words数组中是否有当前子字符串，如果没有，i++，如果存在，再从i+word.length处截取子字符串，以此类推；再判断子字符串是否存在时，可以通过一个map统计每个word出现的次数，遍历时，出现一个word，则对应次数加1，具体看代码实现：

 class Solution {
 public:
     vector<int> findSubstring(string S, vector<string> &L) {
         int l_size = L.size();

         if (l_size <= ) {
             return vector<int>();
         }

         vector<int> result;
         map<string, int> word_count;
         int word_size = L[].size();
         int i, j;

         for (i = ; i < l_size; ++i) {
             ++word_count[L[i]];
         }

         map<string, int> counting;

         for (i = ; i <= (int)S.length() - (l_size * word_size); ++i) {
             counting.clear();

             for (j = ; j < l_size; ++j) {
                 string word = S.substr(i + j * word_size, word_size);

                 if (word_count.find(word) != word_count.end()) {
                     ++counting[word];

                     if (counting[word] > word_count[word]) {
                         break;
                     }
                 }
                 else {
                     break;
                 }
             }

             if (j == l_size) {
                 result.push_back(i);
             }
         }

         return result;
     }
 };