DP 优化方法合集

0. 前言

写完这篇文章后发现自己对于 DP 的优化一窍不通，所以补了补 DP 的一些优化，写篇 blog 总结一下。

1. 单调队列/单调栈优化

1.2 算法介绍

这应该算是最基础的 DP 优化方法了。

顾名思义，单调队列/单调栈优化 DP 就是保持容器内元素的单调性，以达成减少冗余状态的目的。

举单调队列的例子来说，当一个元素的两种属性（例如下标和权值）都优于另一元素时，就可以用此元素更换掉另一元素。这也正是 OI 界流传说法“当一个人比你小且比你强时，你就被弹出单调队列了”的原理。

我们以下面的例题作为例子来更具体地阐述这个算法。

1.3 适用范围&区别

一般来说，形如 \(f(i)=\max(f(j)+F(i)+F(j))\) 的式子都可以考虑适用单调队列/单调栈进行优化。（其中 \(F(i)\) 和 \(F(j)\) 表示和 \(i,j\) 有关的函数）

应该大部分人刚学这两种东西的时候都有一种疑惑：啥时候用单调队列，啥时候用单调栈呢？（至少我有

其实，它们两的本质区别还是其结构上的区别。单调栈通常用新加进来的东西替换掉一些栈顶元素，而单调队列是可能两端同时修改的。

在一下例题中我也会着重分析两者的使用。

1.4 例题

I. P1886 滑动窗口

题目链接

这个不是优化 DP，就是最经典的裸的不能再裸的单调队列。

大力单调队列即可，时间复杂度 \(O(n)\)。

II. CF372C Watching Fireworks is Fun

题目链接

OI Wili 推荐的题

题目大意：一个数轴上有 \(n\) 个点，每个点在位置 \(a_i\)，有 \(m\) 个烟花要放，开始时间 \(t_i\)。你一开始的位置随便，每一单位时间可以最多走 \(d\) 这么多的距离，在 \(x\) 看到第 \(i\) 个烟花的快乐值为 \(b_i-|a_i-x|\)，求最大的总代价。

数据范围：\(n\leq 150000,m\leq 300\)。

看到这个数据范围就知道大概是 \(O(nm)\) 的算法（最多要卡卡常）。

我们容易设计出 DP 状态 \(f(i,j)\) 表示放第 \(i\) 个烟花，位置在 \(j\) 时的最大快乐值。

转移：\(f(i,j)=\max_{j-(t_i-t_{i-1})\cdot d_i\leq k\leq j+(t_i-t_{i-1})\cdot d_i}(f(i-1,k)+b_i-|a_i-j|)\)。

接下来就需要对 DP 进行优化了，首先因为当 \(i\) 和 \(j\) 确定时 \(b_i-|a_i-j|\) 可以看做常数，剩下的就可以用单调队列去维护了。

注：本题使用单调队列的原因为 \(k\) 两边都有限制，需要头尾都更新。

时间复杂度 \(O(nm)\)。

代码

III. P3572 [POI2014]PTA-Little Bird

题目链接

IV. P1973 [NOI2011] NOI 嘉年华

题目链接

V. P2254 [NOI2005] 瑰丽华尔兹

题目链接

2. 斜率优化

斜率优化自己学过好几遍，也听 dalao 讲过，但是总是感觉半懂不懂的。这次索性把它给搞彻底了罢……

2. 1 算法介绍

以 OI Wiki 上的例题为例。

题目大意：有 \(n\) 个玩具，每个玩具有一个价值 \(c_i\)。你需要将这 \(n\) 个玩具分成若干段，设一段 \([l,r]\) 的代价为 \((r-l+\sum_{i=l}^rc_i-L)^2\)，其中 \(L\) 为常数，求最小的总代价。

数据范围：\(n\leq 5\times 10^4\)

使用 DP 优化的一般思路：先设计出一个超时的 DP 再优化。

设 \(f_i\) 表示前 \(i\) 个玩具的代价，那么得出转移方程为：

\[f_i=\min_{j=0}^{i-1}\{f_j+(i-j-1+\sum_{k=j+1}^ic_k+L)^2\}
\]

用前缀和表示后即为：

\[f_i=\min_{j=0}^{i-1}\{f_j+(i-j-1+S_i-S_j+c_k+L)^2\}
\]

其中 \(S_i=\sum_{k=1}^ic_k\)。

这就是朴素的 \(O(n^2)\) 的 DP。

下面就要优化了，不过有个问题：DP 跟斜率有什么关系呢？

考虑将 DP 转移方程转化为解析几何中直线的斜截式方程 \(y=kx+b\) 的形式。

我们先将只和 \(i,j\) 有关的归为一类，常数归为一类：\(s_i=S_i+i,l=L+1\)，然后原式可以写成：

\[f_i=\min_{j=0}^{i-1}\{f_j+(s_i-s_j-l)^2\}
\]

然后可以令 \(y=f_j+s_j^2,k=-2(l-s_i),x=s_j,b=f_i-(s_i-l)^2\)。(P.S. 这个应该只要满足 \(y=kx+b\) 都可以？)

此时需要最小化直线的截距，先将这些 \((x,y)\) 表示在平面直角坐标系中：

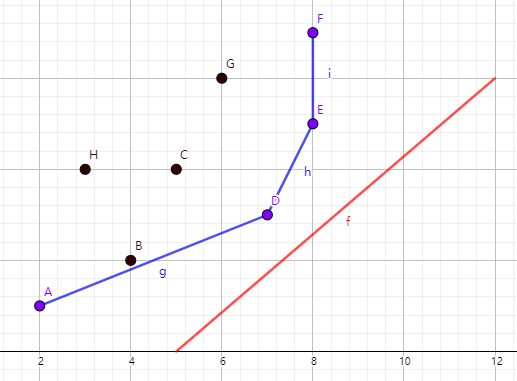
可以看到蓝线连成了一个下凸壳，第一个红线碰到的点使截距最小。