斜率优化 dp 总结

我们以一道例题引入：

洛谷 P2365 任务安排：

---

\(n\) 个任务排成一个序列在一台机器上等待完成（顺序不得改变），这 \(n\) 个任务被分成若干批，每批包含相邻的若干任务。

从零时刻开始，这些任务被分批加工，第 \(i\) 个任务单独完成所需的时间为 \(t_i\)​。在每批任务开始前，机器需要启动时间 \(s\)，而完成这批任务所需的时间是各个任务需要时间的总和（同一批任务将在同一时刻完成）。

每个任务的费用是它的完成时刻乘以一个费用系数 \(C_i\)​。请确定一个分组方案，使得总费用最小。

设 \(dp_i\) 为选取到第 \(i\) 个任务时的最大价值，枚举一个起点 \(j\) 分批可以得到：

\[dp_i=\min\{dp_i,dp_j+\text{sum}_T(1,i)\text{sum}_C(i,j+1)+s\cdot\text{sum}_C(n,j+1)\}
\]

其中对于序列 \(S\)，

\[\text{sum}_S(l,r)=\sum_{i=l}^rS_i=\text{sumS}_r-\text{sumS}_{l-1}
\]

后面这个等号是求法，\(\rm sumS\) 是前缀和，也就是

\[\text{sumS}_i=\sum_{k=1}^iS_i
\]

时间复杂度 \(O(n^2)\) .

Code:

#include<ctime>
#include<queue>
#include<stack>
#include<cmath>
#include<iterator>
#include<cctype>
#include<vector>
#include<map>
#include<set>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<bitset>
using namespace std;
const int N=5005;
int n,s,t[N],c[N],sumT[N],sumC[N],dp[N];
int main()
{
	scanf("%d%d",&n,&s);
	for (int i=1;i<=n;i++)
	{
		scanf("%d%d",t+i,c+i);
		sumT[i]=sumT[i-1]+t[i]; sumC[i]=sumC[i-1]+c[i];
	} memset(dp,0x3f,sizeof dp); dp[0]=0;
	for (int i=1;i<=n;i++)
		for (int j=0;j<i;j++)
			dp[i]=min(dp[i],dp[j]+sumT[i]*(sumC[i]-sumC[j])+s*(sumC[n]-sumC[j]));
	printf("%d",dp[n]);
	return 0;
}

这个 \(O(n^2)\) 的做法还是太慢了，过不了 \(3\times 10^5\) 的数据，考虑优化。

要优化，当然先对动态转移方程变形：

\[\begin{aligned}dp_i&=\min\{dp_i,dp_j+\text{sum}_T(1,i)\text{sum}_C(i,j+1)+s\cdot\text{sum}_C(n,j+1)\}\\&=dp_j-(\text{sumT}_i+s)\text{sumC}_j+\text{sumT}_i\text{sumC}_i+s\cdot\text{sumC}_n&\text{设 }j\text{ 是使得 }dp_i \text{ 取到最小值的 }j\\\Rightarrow dp_j&=(\text{sumT}_i+s)\text{sumC}_j+dp_i-\text{sumT}_i\text{sumC}_i-s\cdot\text{sumC}_n\end{aligned}
\]

此时令 \(\begin{cases}dp_j=y&\text{因变量}\\\text{sumT}_i+s=k&\text{斜率}\\\text{sumC}_j=x&\text{自变量}\\dp_i-\text{sumT}_i\text{sumC}_i-s\cdot\text{sumC}_n=b&\text{截距}\end{cases}\) 可以得到：

\[y=kx+b
\]

发现这正好是一个直线方程，并且 \(x\) 是随着 \(j\) 改变而改变的。

别忘了我们的目标：使 \(dp_i\) 最小，要使 \(dp_i\) 最小，就要让 \(b\)（截距）最小（\(b\) 中除了 \(dp_i\) 以外的东西都是常量）。

我们可以在平面直角坐标系上点出下列点：\((dp_0,\text{sumC}_0),(dp_1,\text{sumC}_1),\cdots,(dp_{i-1},\text{sumC}_{i-1})\) 还有斜率 \(k\) 表示的直线：

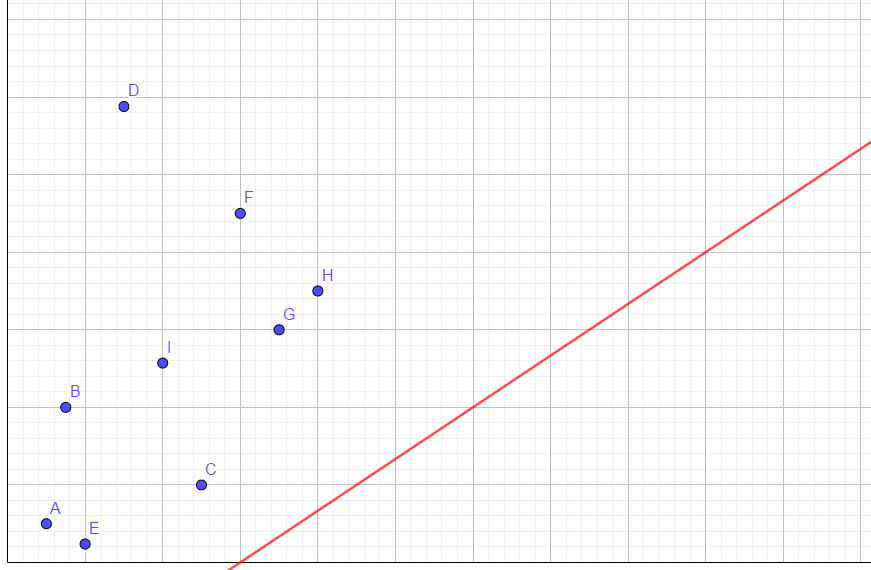
P.S. 以下所有图的横坐标都是 \(\text{sumC}_j\)，纵坐标都是 \(dp_j\) .

我们将 \(b\) 改变，直线将会滑动：

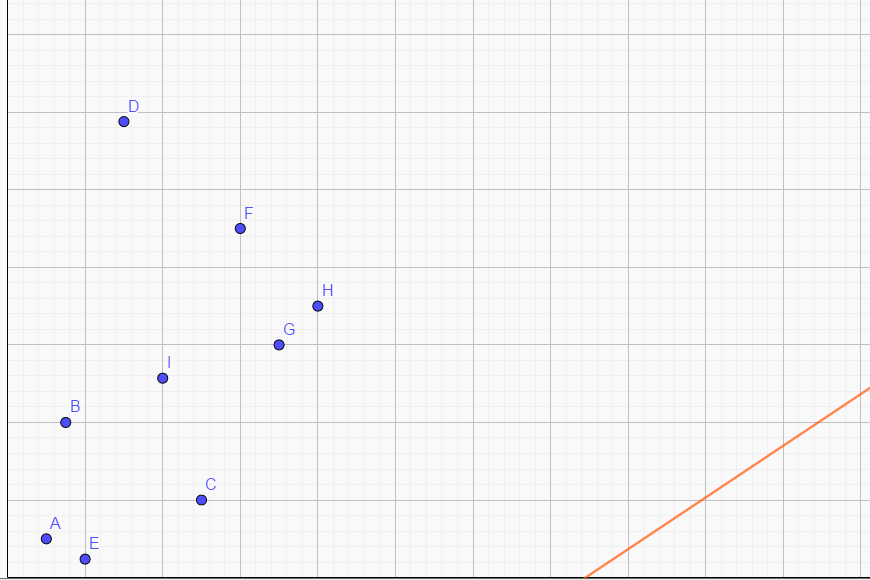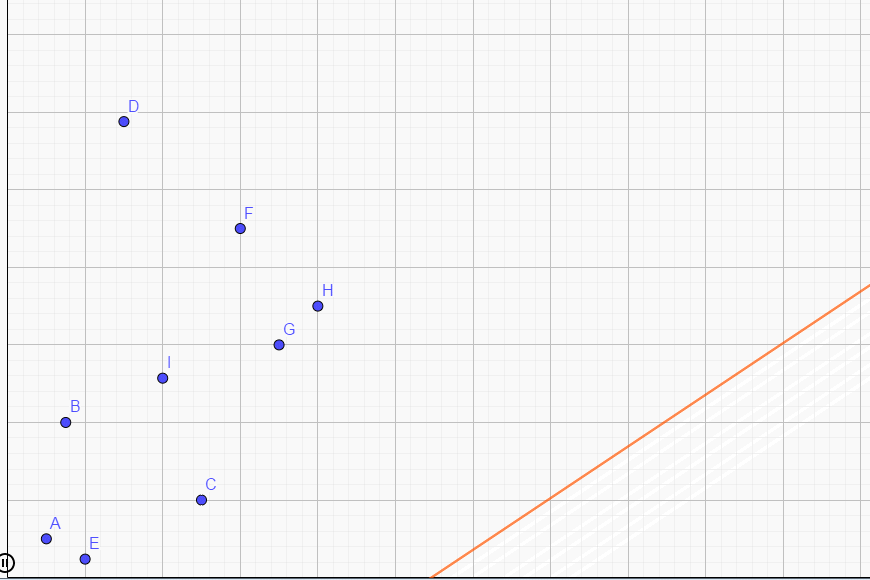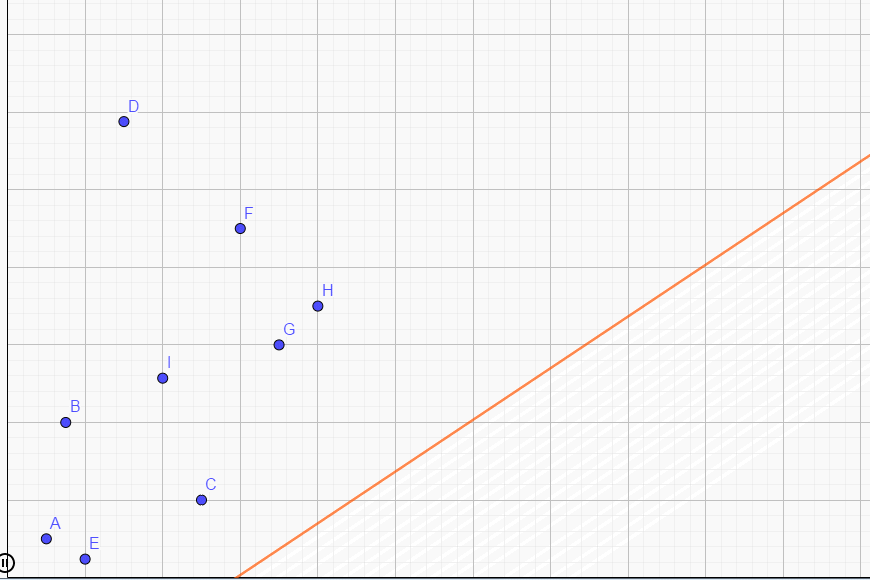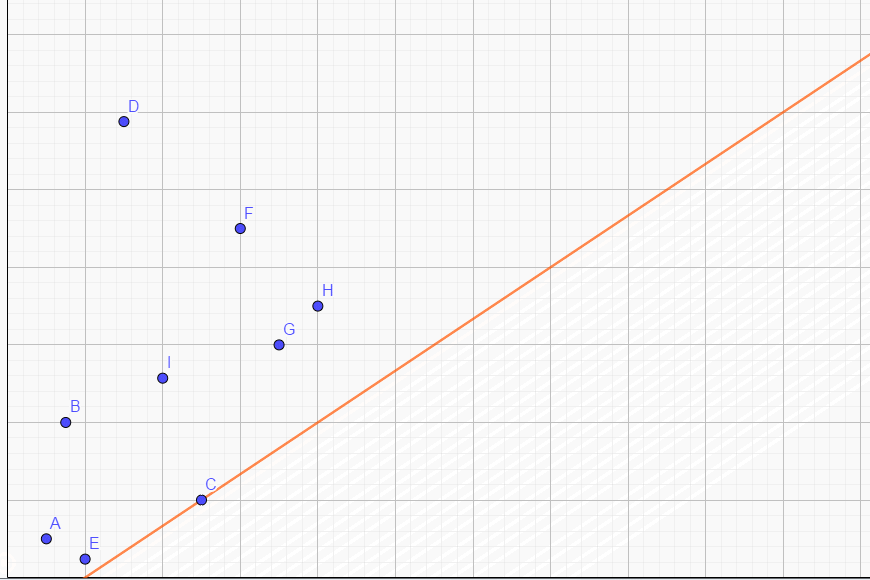
注意最小的 \(j\) 正好就是滑动时第一次遇到的点。

每次更新的时候后面都会插入点，注意到斜率 \(k\) 和插入点的横坐标都是 递增 的，所以我们可以将相邻两点的直线连上，然后把上面的点全部去掉（因为不可能会成为最小的 \(j\) 了）：

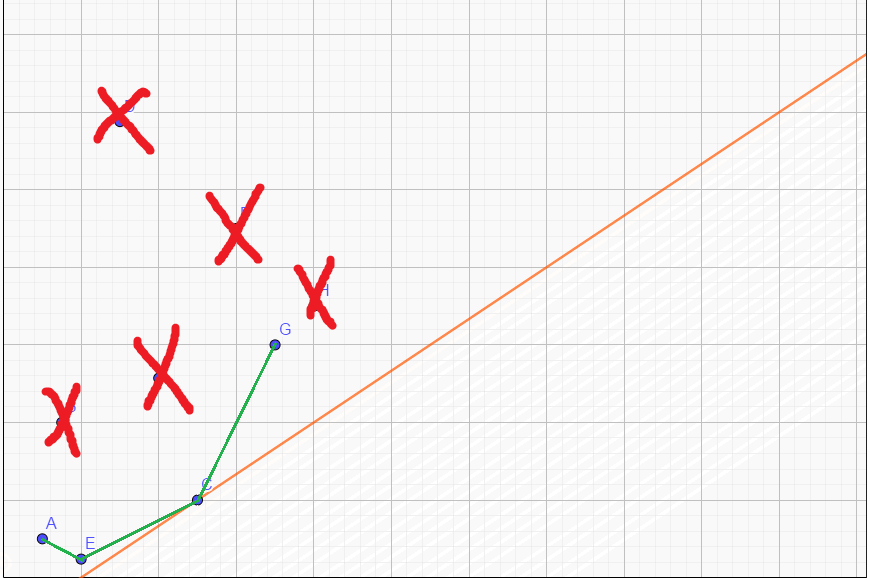
发现绿线那里正好连成了一个下凸壳（凸包的定义：一个多边形是凸包当且仅当对于它的所有边满足所有点都在它所在的直线的一侧）。

现在我们怎么找遇到的第一个点呢？

注意到凸包相邻两点间的的斜率是递增的，手玩或者找规律可以得到答案就是 第一个斜率 \(>k\) 的点 所以我们可以二分。

当然，我们还有一种办法。

这个问题相当于在一个单调队列中找第一个大于 \(k\) 的点。

策略 \(1\)：在查询的时候，可以把队头小于当前斜率的点全部删掉（因为不可能会参与答案了）

策略 \(2\)：在插入的时候，将队尾所有不在凸包（不满足凸包性质）的点全部删掉（不要删掉插入进去的点）

不满足凸包性质的判断是纵坐标高于两点并且横坐标在两点之间，比如下图中，加入新点 \(N\)，这使得 \(G\) 不满足性质，应当删去。

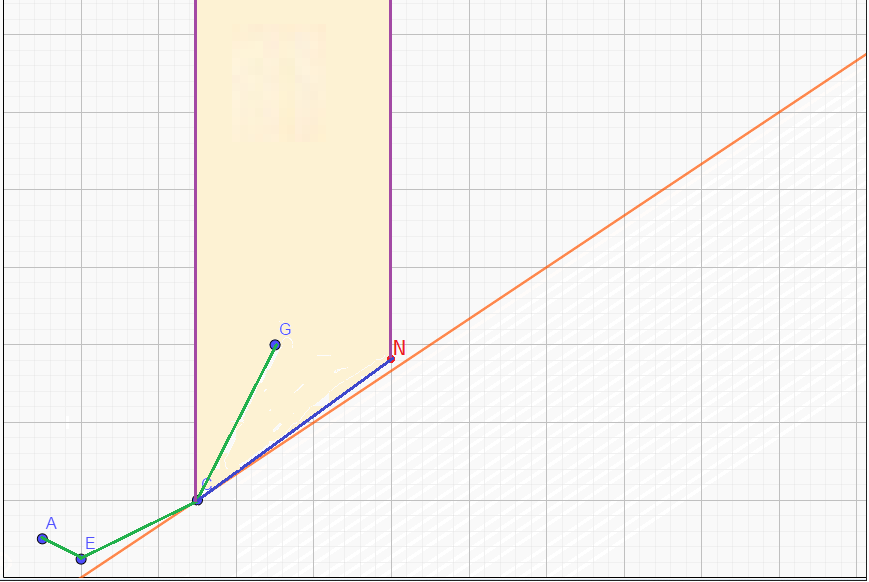
就按这写代码即可，注意条件：

• 策略 \(1\)：\(\dfrac{dp_2-dp_1}{C_2-C_1}\le \text{sumT}_i+s\)
• 策略 \(2\)：\(\dfrac{dp_{tail}-dp_{tail-1}}{C_{tail}-C_{tail-1}}\ge\dfrac{dp_{i}-dp_{tail}}{C_{i}-C_{tail}}\)（其中 \(tail\) 是队尾）

上面是按斜率式写的，应该很容易理解，但是代码里应该注意式子有除法要移项变成乘法减少误差。

Code:

#include<ctime>
#include<queue>
#include<stack>
#include<cmath>
#include<iterator>
#include<cctype>
#include<vector>
#include<map>
#include<set>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<bitset>
using namespace std;
const int N=3e5+5;
typedef long long ll; // 开 long long
int n,s,t[N],c[N];
ll sumT[N],sumC[N],dp[N],q[N];
int main()
{
	scanf("%d%d",&n,&s);
	for (int i=1;i<=n;i++)
	{
		scanf("%d%d",t+i,c+i);
		sumT[i]=sumT[i-1]+t[i]; sumC[i]=sumC[i-1]+c[i]; // 前缀和
	} int head=0,tail=0; // q[0]=0; 这句是隐式的，不用写
	for (int i=1;i<=n;i++)
	{
		while ((head<tail)&&(dp[q[head+1]]-dp[q[head]]<=(sumT[i]+s)*(sumC[q[head+1]]-sumC[q[head]]))) ++head; // 策略 1
		int j=q[head];
		dp[i]=dp[j]+sumT[i]*(sumC[i]-sumC[j])+s*(sumC[n]-sumC[j]); // 转移，此时的 j（也就是 q[head]）已经是最小的 j 了，所以不用加 min 了
		while ((head<tail)&&((dp[q[tail]]-dp[q[tail-1]])*(sumC[i]-sumC[q[tail]])>=
		                     (dp[i]-dp[q[tail]])        *(sumC[q[tail]]-sumC[q[tail-1]]))) --tail; // 策略 2
		q[++tail]=i; // 最后再入队（因为策略 2 里不能把插入的点丢出去）
	}
	printf("%lld",dp[n]);
	return 0;
}

，

如果像 SDOI2012 任务安排 那样，\(T_i\) 是负数（时 间 倒 流），那么单调性就没了，就只能二分了 qwq

将原代码里的

while ((head<tail)&&(dp[q[head+1]]-dp[q[head]]<=(sumT[i]+s)*(sumC[q[head+1]]-sumC[q[head]]))) ++head;
int j=q[head];

换成

int l=head,r=tail;
while (l<r)
{
	int mid=(l+r)>>1;
	if (dp[q[mid+1]]-dp[q[mid]]>(sumT[i]+s)*(sumC[q[mid+1]]-sumC[q[mid]])) r=mid;
	else l=mid+1;
} int j=q[r];

即可。

那么如果 \(C_i\) 是负数呢？

可以倒序 dp，设计一个状态转移方程，让 \(\text{sumT}_i\) 是横坐标，\(\text{sumC}_i\) 是斜率中的一项。仍然可以用单调队列维护凸壳，用二分法求出最优决策。

那么如果 \(T_i,C_i\) 都是负数呢？

可以考虑 cdq 分治或平衡树维护凸包，具体可以参考 NOI2007 货币兑换或者 OI-Wiki。

---

总结一下，斜率优化是解决形如

\[dp_i=\min_{L(i)\le j\le R(i)}\{dp_j+S(i,j)\}
\]

其中 \(L(i),R(i)\) 是关于 \(i\) 的一次函数，\(S(i,j)\) 是关于 \(i,j\) 的多项式（可以有 \(i,j\) 的乘积项）。

（这好像也叫 1D/1D 型转移？）

还有一个特点：斜率优化的转移方程一般很复杂 qwq

---

习题：Codeforces 311B Cats Transport