Spark机器学习(8)：LDA主题模型算法

1. LDA基础知识

LDA（Latent Dirichlet Allocation）是一种主题模型。LDA一个三层贝叶斯概率模型，包含词、主题和文档三层结构。

LDA是一个生成模型，可以用来生成一篇文档，生成时，首先根据一定的概率选择一个主题，然后在根据概率选择主题里面的一个单词，这样反复进行，就可以生成一篇文档；反过来，LDA又是一种非监督机器学习技术，可以识别出大规模文档集或语料库中的主题。

LDA原始论文给出了一个很简单的例子。Arts、Budgets、Children、Education是4个主题，下面是每一个主题包含的单词。

然后就可以随机选择主题，以及每个主题里面的单词，重复多次后就生成了一篇文档，其中不同的颜色表示单词来自不同的主题。

可见，文档和单词是可见的，而主题是隐藏的。

文档里某个单词出现的概率可以用公式表示：

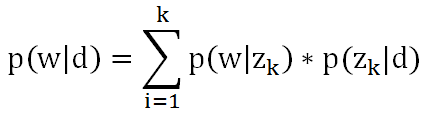
其中d是文档，w是单词，z是主题，k是主题数量。可以想象成三个矩阵：

第一个矩阵表示每个文档里面每个单词出现的概率，第二个矩阵表示每个文档里面每个主题出现的概率，第三个矩阵表示每个主题里面每个词语出现的概率。在机器学习时，根据文档集，我们可以计算出第一个矩阵，要求的是第二个矩阵和第三个矩阵。

2. 极大似然估计

极大似然估计的基本思想是，从总体抽取n个样本之后，最合理的参数估计量应该是使得这批样本出现的概率最大的参数估计量。比如说你在一个小城市，很少看见美国人，偶然看见了几个美国人身材都很高，这时就可以估计美国人普遍身材很高，因为只有这样你看到几个美国人身材都很高这件事出现的概率才最大。

3. EM方法

EM即Exception Maximization，是机器学习的重要算法之一，在机器学习中有着重要的作用。简单的说，EM方法就是解决这样的问题：想估计两个参数A和B，这两个参数都是未知的，知道了参数A就能得到参数B，反过来知道了参数B就能得到参数A，这时我们就可以先给A一个初始值，然后计算出B，然后再根据计算出的B再计算A，这样反复迭代下去，一直到收敛为止。在数学上可以证明这种方法时有效的。

4. Beta分布和Dirichlet分布

Beta分布是二项分布的共轭先验分布：

比如抛硬币，3次出现正面，2次出现背面，a=3，b=2，就可以得到一个概率分布图，从概率分布图上可以看出，x=0.6时函数取得最大值，于是就可以认为x的值很可能接近于0.6，又扔了5次，2次正面，3次背面，a=5，b=5，又可以得到一个新的概率分布图，x=0.5时函数取得最大值，此时可以认为x的值很可能接近于0.5。

Dirichlet分布和Beta分布类似，是Beta分布在高维度的推广：

比如扔骰子，扔了60次，6个面，各出现10次，可以得到一个概率分布图，x=(1/6,1/6,1/6,1/6,1/6,1/6)时函数取得最大值，x的值很可能接近于(1/6,1/6,1/6,1/6,1/6,1/6)。

5. LDA的EM算法

具体到LDA，采用EM方法的步骤如下：

(1) 给矩阵wk和kj随机赋值，其中wk是每个主题中每个单词出现的次数，kj是每个文档中每个主题出现的次数，虽然这些次数还只是随机数，我们还是可以根据这些次数，利用Dirichlet分布计算出每个主题中每个单词最可能出现的概率，以及每个文档中每个主题最可能出现的概率，也就相当于给上面的第二个和第三个矩阵初始值；

(2) 对于文档中的一个单词，计算出是由哪个主题产生的，因为可能有多个主题都会产生这个单词，那么它到底是属于哪个主题呢？这时就要用到极大似然估计了。计算出每个主题产生这个单词的概率：

然后找出概率最大的那个主题，认为这个单词就是这个主题产生的，这在EM方法中属于E-STEP；

(3) 由于确定了这个单词是哪个主题产生的，相当于Dirichlet分布中a的值发生了改变，于是计算出新的概率矩阵（即上面的第二个和第三个矩阵），这在EM方法中属于M-STEP。

重复步骤(2)和(3)，就可以得到最终的概率矩阵（即上面的第二个和第三个矩阵），机器学习结束。

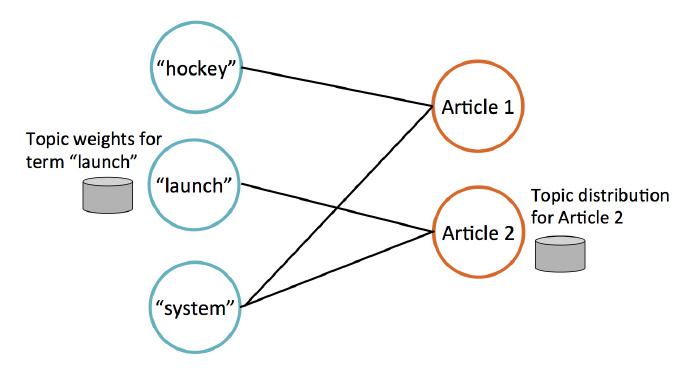
6. MLlib中LDA的实现

MLlib使用GraphX实现LDA。有两类节点：词节点和文档节点。每个词节点上存储一个单词，以及这个单词属于每一个主题的概率；每个文档节点上存储一个文档，以及这个文档属于每个主题的概率。例如下图，存储了3个单词和两个文档，hockey和system在Article1中出现，launch和system在Article2中出现。

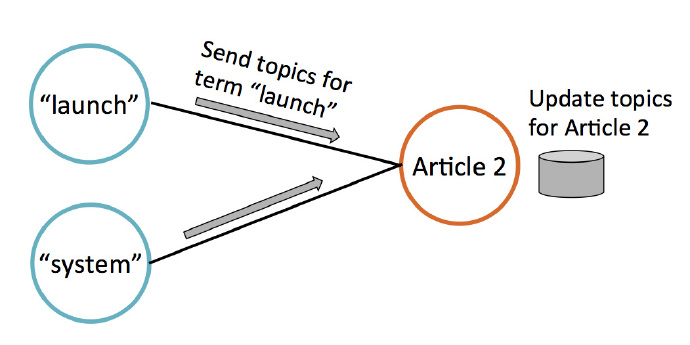
迭代过程中，文档节点通过收集邻居节点（即词节点）的数据来更新自己的主题概率，如下图所示。