mod(%)之规律(除数与被除数的正负分析)

首先注意“-9 % 4”，根据运算符优先级，负号运算符优先级大于余数（取模），所以执行的是“(-9) % 4”。

其次 % = mod ，只是在不同地方表示方法不同而已。

被除数无论是正数和负数结果都一样，所以可以把负数的被除数看成是正数。

若除数为负数，结果与除数为正数相比多了一个负号。

x % y = abs(x) % abs(y) * (x>0)

abs : 绝对值，如abs(-5)=5，abs(5)=5

(x>0) : 若x>0,结果为1，否则结果为0

如:

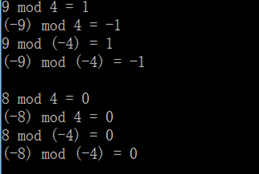
9 % 4 = 9 % 4 * 1 = 1

(-9) % 4 = 9 % 4 * (-1) = -1

9 % (-4) = 9 % 4 * 1 = 1

(-9) % (-4) = 9 % 4 * (-1) = -1

 #include <stdio.h>
 #include <stdlib.h>

 int main()
 {
     printf("9 mod 4 = %d\n", % );
     printf("(-9) mod 4 = %d\n",(-) % );
     printf("9 mod (-4) = %d\n", % (-));
     printf("(-9) mod (-4) = %d\n",(-) % (-));

     printf("\n");

     printf("8 mod 4 = %d\n", % );
     printf("(-8) mod 4 = %d\n",(-) % );
     printf("8 mod (-4) = %d\n", % (-));
     printf("(-8) mod (-4) = %d\n",(-) % (-));

     return ;
 }