pde复习笔记 第一章 波动方程 第三节 分离变量法

教材

谷超豪《数学物理方程》第四版，虽然我们老师用的第三版，但是除了页码对不上，习题多了一点，也似乎没有多少区别。

打算开个新栏专门总结一下pde的各种计算问题，在图书馆算的手麻了，但是习题几乎都是按套路出牌，所以打算好好总结一下。

• 齐次方程
  
  
  
  
  
  
  
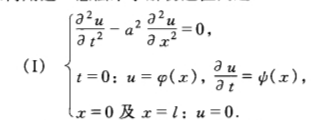
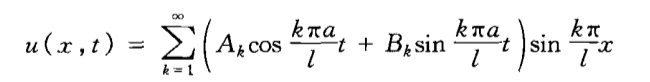
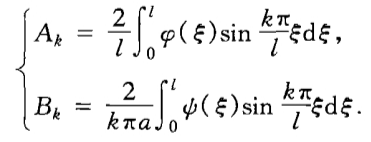
  提醒：这里的边界条件是两端固定，也即\(u(0,t)=u(l,t)=0\)，对应的解里面是\(\dfrac{k\pi}{l}\)，做题的时候还会遇见\(u(0,t)=\dfrac{\partial u}{\partial x}(l,t)=0\)，这个时候对应的就是\(\dfrac{(k+\frac{1}{2})\pi}{l}\),一定注意。（可以自己算一下为什么多了\(\frac{1}{2}\pi\)）
  
  例题（习题第1题）
  
  
  
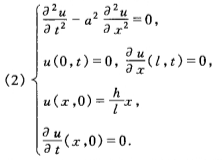
  解答
  
  

\[A_{k}=\frac{2}{l}\int _{0}^{l}\dfrac{hx}{l}\sin(\dfrac{(k+\frac{1}{2})\pi x }{l} )dx=\dfrac{(-1)^{k}2h}{(k+\frac{1}{2})^{2}\pi^{2}}
\]

\[B_{k}=0
\]

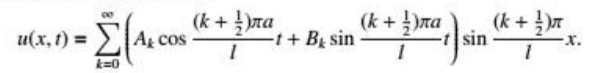
我们上面介绍的是用积分法计算系数\(A_{k}, B_{k}\), 而边值条件很特殊的时候，我们有一个更简单的计算方法。

例题（习题第3题）



本题的特殊之处就在于边值条件是\(x\)的正弦函数，我们在计算系数\(A_{k}, B_{k}\)的时候，可以不使用积分，而是直接比较系数。

• 非齐次方程
  
  
  
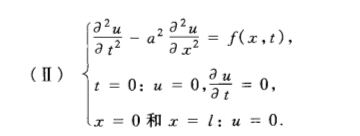
  的解有如下形式：
  
  
  
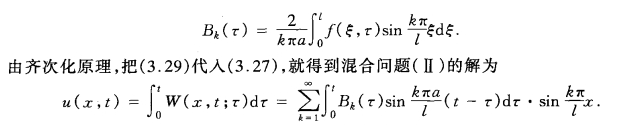
  简单而言计算的套路就是先计算\(B_{k}(\tau)\), 再代入即可
  
  例题（课后题第4、5题），我们以第四题为例子。
  
  
  
  首先利用叠加原理，拆成两个式子：

\[\left\{
\begin{array}{l}
u_{tt} - a^2 u_{xx} = 0, 0 < x < l, t > 0, \\
\left.u\right|_{x=0} = \left.u_{x}\right|_{x=l} = 0, \\
\left.u\right|_{t=0} = 0, \left.u_{t}\right|_{t=0} = \sin \frac{\pi x}{2l},
\end{array}
\right.\]

这是前面常规的计算套路（比较系数就可以了），解为

\[u_{1}(x, t) = \frac{2l}{\pi a} \sin \frac{\pi a}{2l} t \sin \frac{\pi}{2l} x
\]

现在我们考虑

\[\left\{
\begin{array}{l}
u_{tt} - a^2 u_{xx} = g, 0 < x < l, t > 0, \\
\left.u\right|_{x=0} = \left.u_{x}\right|_{x=l} = 0, \\
\left.u\right|_{t=0} = 0, \left.u_{t}\right|_{t=0} = 0,
\end{array}
\right.
\]

利用上面给出的公式，直接计算

\[B_{k}(\tau)=\dfrac{2}{(k+\frac{1}{2})\pi a }\int _{0}^{l}g \sin (\dfrac{(k+\frac{1}{2})\pi x}{l})dx=\dfrac{2gl}{a\pi ^{2}(k+\frac{1}{2})^{2}}
\]

\[u_{2}(x, t) = \int_{0}^{t} \sum_{k=0}^{\infty} \frac{2l g}{\pi^{2} a\left(k+\frac{1}{2}\right)^{2}} \sin \frac{k+\frac{1}{2}}{l} \pi a(t-\tau) \sin \frac{k+\frac{1}{2}}{l} \pi x \mathrm{~d} \tau .
\]

综上，原问题的解为$$u(x, t) = u_{1}(x, t) + u_{2}(x, t)$$.

• 一道特殊的习题（习题第6题）

6.用分离变量法求下面问题的解:

\[\left\{
\begin{array}{l}
\frac{\partial^{2} u}{\partial t^{2}}+2 b \frac{\partial u}{\partial t}=a^{2} \frac{\partial^{2} u}{\partial x^{2}} \quad(b>0), \\
\left.u\right|_{x=0}=\left.u\right|_{x=l}=0, \\
\left.u\right|_{t=0}=\frac{h}{l} x, \left.\frac{\partial u}{\partial t}\right|_{t=0}=0 .
\end{array}
\right.
\]

对于本题，陈恕行的数学物理方程中有过专门的讨论

至此，我们就将本节所有习题讨论完了。无一例外都是套公式计算。