【matplotlib 实战】--箱型图

箱型图（Box Plot），也称为盒须图或盒式图，1977年由美国著名统计学家约翰·图基（John Tukey）发明。
是一种用作显示一组数据分布情况的统计图，因型状如箱子而得名。

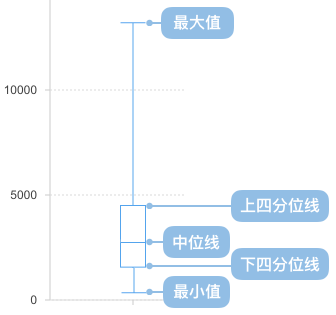
它能显示出一组数据的最大值、最小值、中位数及上下四分位数。
箱子的顶端和底端，分别代表上下四分位数。
箱子中间的是中位数线，它将箱子一分为二。从箱子延伸出去的线条展现出了上下四分位数以外的数据，由于这两根延伸出去的线像是胡须，因此箱形图也被称为盒须图。

箱形图最大的优势是，它以一种简单的方式，概括出一个或多个数值变量的分布，同时又不会占据太多空间。

1. 主要元素

它主要由以下五个元素组成：

1. 最大值：表示数据的最大值，排除了异常值后的上限。
2. 上四分位线：数据的上四分位数，将数据分为四等份，处于上边缘和中位数之间的数据。也称为第三四分位数。
3. 中位数：数据的中位数，将数据分为两等份，处于上四分位数和下四分位数之间的数据。也称为第二四分位数。
4. 下四分位线：数据的下四分位数，将数据分为四等份，处于中位数和下边缘之间的数据。也称为第一四分位数。
5. 最小值：表示数据的最小值，排除了异常值后的下限。

2. 适用的场景

箱型图适用于以下分析场景：

• 数据分布比较：比较不同组数据的分布情况。通过将多个箱型图放在一起，可以直观地比较它们的中位数、四分位数和离群值等信息，从而了解它们之间的差异。
• 离群值检测：检测数据中的离群值。离群值是与其他数据点相比明显偏离的数据点，它们可能是数据收集或记录过程中的异常或错误。箱型图中的离群点可以帮助识别这些异常值。
• 数据中心趋势和离散程度：通过中位数和四分位距（上四分位数与下四分位数之差）展示了数据的中心趋势和离散程度。中位数提供了数据的中心位置，四分位距提供了数据的离散程度。
• 数据分布形状：提供关于数据分布形状的一些信息。例如，如果箱型图的上下边缘和中位数都接近，箱型图可能显示出对称的分布。如果箱型图的上边缘比下边缘长，中位数偏向下边缘，可能显示出右偏分布。

3. 不适用的场景

箱型图不适用于以下分析场景：

• 数据样本过小：当数据样本过小时，箱型图可能无法提供足够的信息来准确描述数据的分布情况。
• 数据分布复杂：当数据分布非常复杂或包含多个峰值时，箱型图可能无法完全捕捉到数据的特征。
• 数据缺失：如果数据中存在大量缺失值，箱型图可能无法提供准确的分布信息。

4. 分析实战

本次通过箱型图分析我国三大产业对GDP的贡献情况。

4.1. 数据来源

数据来自国家统计局公开的历年数据，整理好的文件从下面的地址下载：
https://databook.top/nation/A02

使用的是其中的 A0201.csv 文件（国内生产总值）

fp = "d:/share/data/A0201.csv"

df = pd.read_csv(fp)
df

4.2. 数据清理

过滤出三大产业在2013年~2022年的增加值数据。

data = df[df["zb"].isin(["A020103",
                         "A020104",
                         "A020105"])].copy()
data = data[data["sj"] > 2012]
data

其中，A020103，A020104，A020105 分别是三大产业的指标编号。

4.3. 分析结果可视化

通过箱型图展示三大产业的增加值情况：

fig = plt.figure()
ax = fig.add_axes([0.1, 0.1, 1, 1])

graph = ax.boxplot(
    [
        data[data["zb"] == "A020103"].loc[:, "value"],
        data[data["zb"] == "A020104"].loc[:, "value"],
        data[data["zb"] == "A020105"].loc[:, "value"],
    ],
    vert=True,
    patch_artist=True,
    labels=["第一产业", "第二产业", "第三产业"]
)
ax.set_title("2013~2022 三大产业对GDP增加值(亿元)")

colors = ['pink', 'lightblue', 'lightgreen']
for patch, color in zip(graph['boxes'], colors):
    patch.set_facecolor(color)

plt.show()

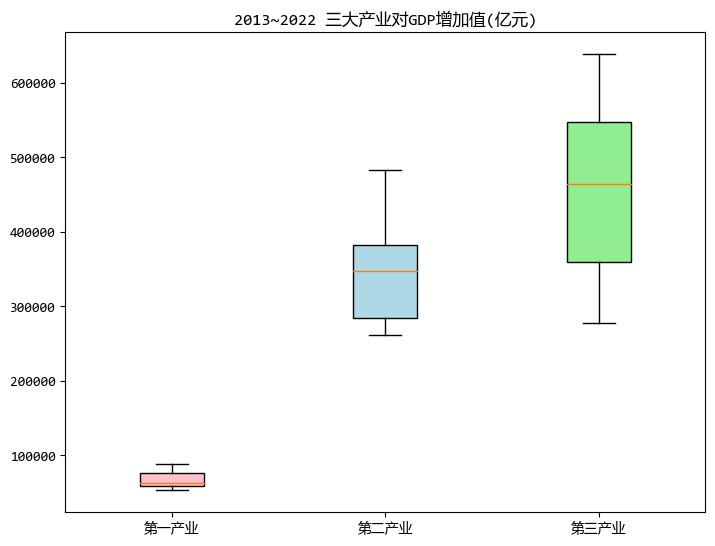
从图中可以看出，近10年来，第一产业的增加值明显低于其他两个产业。
第二第三产业的上下限的值相差比较大，说明增长或者下降比较明显（看了数据，是增长明显）。
第一产业的中位数（红色的横线）偏下半部分，说明多数的年份增加值比较低；
第二产业的中位数（红色的横线）偏上半部分，说明多数的年份增加值比较高。