PID控制器开发笔记之一：PID算法原理及基本实现

在自动控制中，PID及其衍生出来的算法是应用最广的算法之一。各个做自动控制的厂家基本都有会实现这一经典算法。我们在做项目的过程中，也时常会遇到类似的需求，所以就想实现这一算法以适用于更多的应用场景。

1、PID算法基本原理

PID算法是控制行业最经典、最简单、而又最能体现反馈控制思想的算法。对于一般的研发人员来说，设计和实现PID算法是完成自动控制系统的基本要求。这一算法虽然简单，但真正要实现好，却也需要下一定功夫。首先我们从PID算法最基本的原理开始分析和设计这一经典命题。

PID算法的执行流程是非常简单的，即利用反馈来检测偏差信号，并通过偏差信号来控制被控量。而控制器本身就是比例、积分、微分三个环节的加和。其功能框图如下：

根据上图我们考虑在某个特定的时刻t，此时输入量为rin(t)，输出量为rout(t)，于是偏差就可计算为err(t)=rin(t)-rout(t)。于是PID的基本控制规律就可以表示为如下公式：

其中Kp为比例带，T_I为积分时间，T_D为微分时间。PID控制的基本原理就是如此。

2、PID算法的离散化

上一节简单介绍了PID算法的基本原理，但要在计算机上实现就必须将其离散化，接下来我们就说一说PID算法的离散化问题。在实现离散化之前，我们需要对比例、积分、微分的特性做一个简单的说明。

比例就是用来对系统的偏差进行反应，所以只要存在偏差，比例就会起作用。积分主要是用来消除静差，所谓静差就是指系统稳定后输入输出之间依然存在的差值，而积分就是通过偏差的累计来抵消系统的静差。而微分则是对偏差的变化趋势做出反应，根据偏差的变化趋势实现超前调节，提高反应速度。

在实现离散前，我们假设系统采样周期为T。假设我们检查第K个采样周期，很显然系统进行第K次采样。此时的偏差可以表示为err(K)=rin(K)-rout(K)，那么积分就可以表示为：err(K)+ err(K+1)+┈┈，而微分就可以表示为：(err(K)- err(K-1))/T。于是我们可以将第K次采样时，PID算法的离线形式表示为：

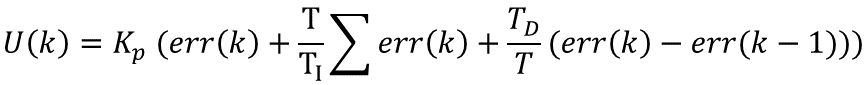
也可以记为：

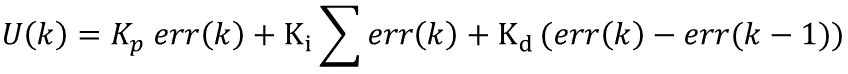
这就是所谓的位置型PID算法的离散描述公式。我们知道还有一个增量型PID算法，那么接下来我们推到一下增量型PID算法的公式。上面的公式描述了第k个采样周期的结果，那么前一时刻也就是k-1个采样周期就不难表示为：

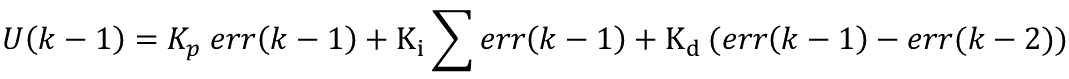
那么我们再来说第K个采样周期的增量，很显然就是U(k)-U(k-1)。于是我们用第k个采样周期公式减去第k-1个采样周期的公式，就得到了增量型PID算法的表示公式：

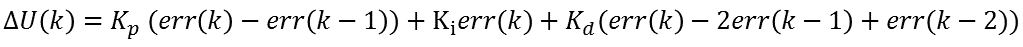
当然，增量型PID必须记得一点，就是在记住U(k)=U(k-1)+∆U(k)。

3、PID控制器的基本实现

完成了离散化后，我们就可以来实现它了。已经用离散化的数据公式表示出来后，再进型计算机编程已经不是问题了。接下来我们就使用C语言分别针对位置型公式和增量型公式来具体实现。

（1）位置型PID的简单实现

位置型PID的实现就是以前面的位置型公式为基础。这一节我们只是完成最简单的实现，也就是将前面的离散位置型PID公式的计算机语言化。

首先定义PID对象的结构体：

 /*定义结构体和公用体*/

 typedef struct

 {

   float setpoint;       //设定值

   float proportiongain;     //比例系数

   float integralgain;      //积分系数

   float derivativegain;    //微分系数

   float lasterror;     //前一拍偏差

   float result; //输出值

   float integral;//积分值

 }PID;

接下来实现PID控制器：

 void PIDRegulation(PID *vPID, float processValue)

 {

   float thisError;

   thisError=vPID->setpoint-processValue;

   vPID->integral+=thisError;

   vPID->result=vPID->proportiongain*thisError+vPID->integralgain*vPID->integral+vPID->derivativegain*(thisError-vPID->lasterror);

   vPID->lasterror=thisError;

 }

这就实现了一个最简单的位置型PID控制器，当然没有考虑任何干扰条件，仅仅只是对数学公式的计算机语言化。

（2）增量型PID的简单实现

增量型PID的实现就是以前面的增量型公式为基础。这一节我们只是完成最简单的实现，也就是将前面的离散增量型PID公式的计算机语言化。

首先定义PID对象的结构体：

 /*定义结构体和公用体*/

 typedef struct

 {

   float setpoint;       //设定值

   float proportiongain;     //比例系数

   float integralgain;      //积分系数

   float derivativegain;    //微分系数

   float lasterror;     //前一拍偏差

   float preerror;     //前两拍偏差

   float deadband;     //死区

   float result; //输出值

 }PID;

接下来实现PID控制器：

void PIDRegulation(PID *vPID, float processValue)

{

  float thisError;

  float increment;

  float pError,dError,iError;

  thisError=vPID->setpoint-processValue; //得到偏差值

  pError=thisError-vPID->lasterror;

  iError=thisError;

  dError=thisError-*(vPID->lasterror)+vPID->preerror;

  increment=vPID->proportiongain*pError+vPID->integralgain*iError+vPID->derivativegain*dError;   //增量计算

  vPID->preerror=vPID->lasterror;  //存放偏差用于下次运算

  vPID->lasterror=thisError;

  vPID->result+=increment;

}

这就实现了一个最简单的增量型PID控制器，也没有考虑任何的干扰条件，仅仅只是对数学公式的计算机语言化。

4、基本特点

前面讲述并且实现了PID控制器，包括位置型PID控制器和增量型PID控制器。界限来我们对这两种类型的控制器的特点作一个简单的描述。

位置型PID控制器的基本特点：

• 位置型PID控制的输出与整个过去的状态有关，用到了偏差的累加值，容易产生累积偏差。
• 位置型PID适用于执行机构不带积分部件的对象。
• 位置型的输出直接对应对象的输出，对系统的影响比较大。

增量型PID控制器的基本特点：

• 增量型PID算法不需要做累加，控制量增量的确定仅与最近几次偏差值有关，计算偏差的影响较小。
• 增量型PID算法得出的是控制量的增量，对系统的影响相对较小。
• 采用增量型PID算法易于实现手动到自动的无扰动切换。

 欢迎关注：