【BZOJ2190】【Luogu P2158】 [SDOI2008]仪仗队

前言：

更不好的阅读

这篇题解真的写了很久，改了又改才成为这样的，我不会写题解但我正在努力去学，求通过，求赞。。。

题目：

BZOJ

Luogu

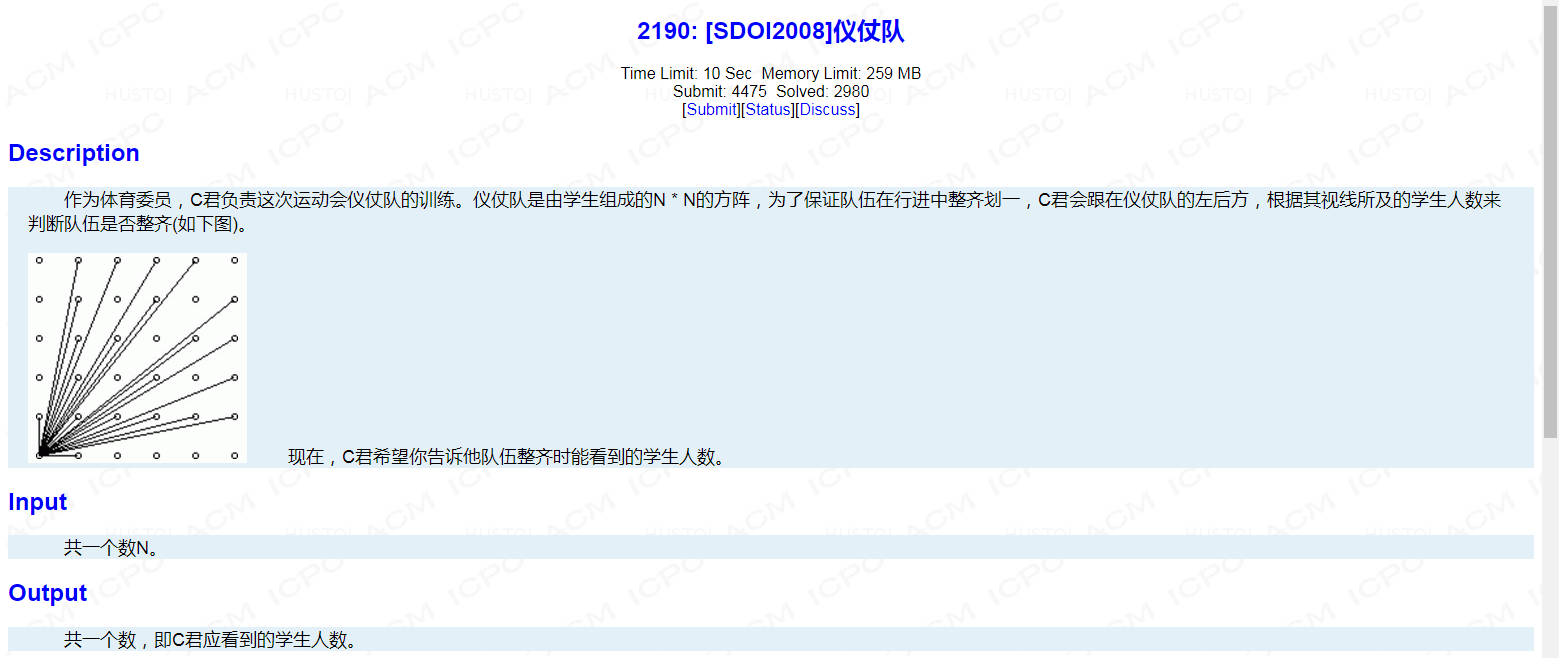
思路：

像我这样的数论菜鸡就不能一秒切这题，怎么办呢？

拿个栗子手玩一下：

假设\(n=6\)，我们看看主人公可以看到的人的位置和他自己的位置有什么关系

随便选几个点,\((1,4),(2,6),(4,4)\),主人公在\((6,1)\)

经过大于几分钟的时间，我发现了一个性质

\[|~x-x'~|\text{和}|~y-y'~|\text{互质时就能看到(设(x,y)表示主人公位置,(x',y')表示某同学位置)}\]

这样我们就可以枚举\(x-x'\)的值和\(y-y'\)的值了， 但是时间爆炸：

怎么办呢？

\(1 \leq N \leq 40000\)这里的话我们原来的\(O(n^2)\)是肯定过不了的，有没有比较快的做法？？？

废话肯定有啊不然这题出出来了

对噢，我们可以用欧拉函数来做呀！

下面有一篇写得比较好的洛谷日报链接，请先阅读完本篇题解，感兴趣的再点

點❤開❤有❤驚❤喜

再给你们看一个东西：

它逆时针旋转45°后左右对称了！

也就是说它拥有对称性。

先放着不管（那你为什么现在放粗来呀）

上面说了，如果要看得到那么要满足\(gcd(|~x-x'~|~,~|~y-y'~|) =1\)。

我们假设\(|~x-x'~|~<~|~y-y'~|\)。

如果我们固定了\(|~y-y'~|\)要找满足条件的\(|~x-x'~|\)。那么这样一来答案不就是\(3+2*\sum_{i=2}^{n-1}\varphi (i)\)了?（这里乘\(2\)是因为我们只做了当\(|~x-x'~|~<~|~y-y'~|\)的部分，又因上文写道这满足对称性所以我们可以乘\(2\)。加\(3\)是因为我们特判了\((0,1),(1, 0),(1,1)\)这\(3\)点。）

对于\(\varphi\)函数，\(\varphi (i)\)表示小于i，且和i互质的数的个数，好了，你看完这句你就可以点开上面那条链接了。

我们可以用一个\(O(n~log~n)\)的埃氏筛去预处理\(\varphi\)函数(见代码部分)，或者使用一个\(O(n)\)的来预处理（请自行翻阅资料）。

代码：

关于埃氏筛\(\varphi\)函数：

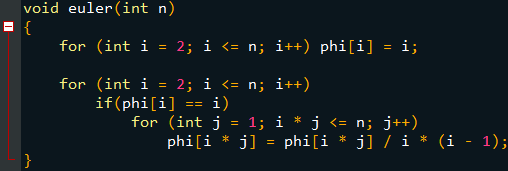
主程序（哎呀，\(\texttt{int main()}\)没截到QAQ）：

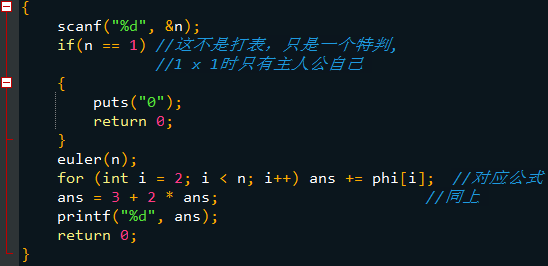
❤感谢收看❤