如何选择梯度下降法中的学习速率α（Gradient Descent Learning Rate Alpha）

梯度下降算法的任务是寻找参数θ，使之能够最小化损失函数。

那么梯度下降法中的学习速率α应该如何选择呢？通常我们画出损失函数随迭代次数增加而变化的曲线。

可能会得到如下的一条曲线，x轴表示迭代次数，y轴表示梯度下降算法迭代相应次数之后算出的损失函数值。

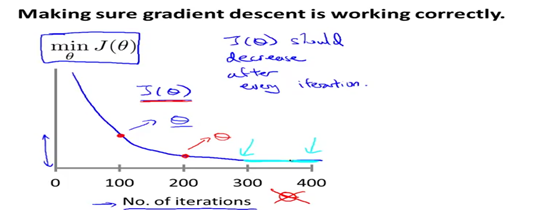
可以看到，当迭代300次之后，损失函数的值并没有下降多少，也就是说在这里梯度下降算法基本上已经收敛了。因此，这条曲线还可以帮助你判断梯度下降算法是否已经收敛。（对于某一个特定的问题，梯度下降算法所需要的迭代次数相差很大，可能对于某一个问题只需要30步，但是对于另一个问题则需要30000步，我们没有办法提前进行判断。）

如果梯度下降算法工作正常，那么每一步迭代之后，损失函数的值都应该下降。

如下图左上角所示，如果你发现随着迭代次数的增加，损失函数的值在变大，这通常是因为学习速率α选择的太大，需要将它调小。（如下图右面所示，我们从初始θ出发，但是由于学习速率α太大，一下子跑到了最低点的左边，然后下一次迭代又一下子跑到了最低点的右边，如此往复，损失函数就会越来越大。）

如下图左下角所示，你也会遇到这样的一种情况：随着迭代次数的增加，损失函数的值一会上升，一会下降，这通常也是因为学习速率α太大，需要使用较小的学习速率。

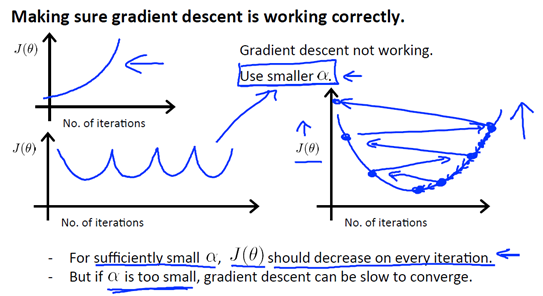
总结来说，如果学习速率α太小，梯度下降收敛速度会很慢；如果学习速率α太大，损失函数的值在每次迭代后不一定能下降，算法最后可能会发散。对于学习速率α，可以先选择0.001，然后按10倍来进行调整。