SOTA激活函数学习

除了之前较为流行的RELU激活函数，最近又新出了几个效果较好的激活函数

一、BERT激活函数 - GELU（gaussian error linear units）高斯误差线性单元

数学公式如下：

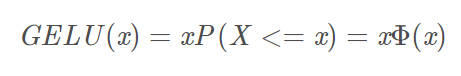
　　X是服从标准正态分布的变量。

近似的数学计算公式如下：

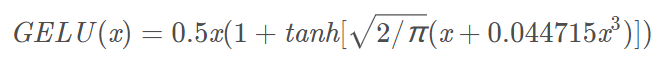
函数图如下：

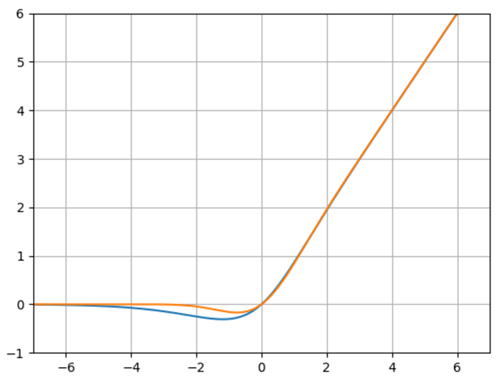
橙色曲线为：GELU

蓝色曲线为：Mish函数

特性：当输入x减小的时候，输入会有一个更高的概率被dropout掉，这样的激活变换就会随机依赖于输入了，在激活中引入了随机正则的思想，是一种对神经元输入的概率描述。但是其实GELU相比Mish函数就要差一点，首先在大于0阶段，Mish函数的梯度是要略大于GELU,在负轴阶段Mish函数比GELU要晚一点趋近于0，也就是神经元能够晚一点死掉。

import math
import numpy as np
from matplotlib import pyplot as plt

def mish(x):
    return x * math.tanh(math.log(1+math.exp(x)))

def GELU(x):
    return 0.5*x*(1+math.tanh(math.sqrt(2/math.pi)*(x+0.044715*x**3)))

x = np.linspace(-10,10,1000)
y=[]
z=[]
for i in x:
    y.append(mish(i))
    z.append(GELU(i))
plt.plot(x,y)
plt.plot(x,z)
plt.grid()
plt.ylim(-1,6)
plt.xlim(-7,7)
plt.show()

二、Mish激活函数

公式如下：

函数图如下：

橙色曲线为：ln(1+e^(x))

蓝色曲线为：Mish函数

import math
import numpy as np
from matplotlib import pyplot as plt

def mish(x):
    return x * math.tanh(math.log(1+math.exp(x)))

def ln_e(x):
    return math.log(1+math.exp(x))

x = np.linspace(-10,10,1000)
y=[]
z=[]
for i in x:
    y.append(mish(i))
    z.append(ln_e(i))
plt.plot(x,y)
plt.plot(x,z)
plt.grid()
plt.show()