浅谈压缩感知（十六）：感知矩阵之RIP

在压缩感知中，总是看到"矩阵满足RIP"之类的字眼，没错，这是一个压缩感知绕不开的术语，有限等距性质（Restricted Isometry Property, RIP）。

注意：RIP性质针对的同样是感知矩阵而非测量矩阵。

0、相关概念与符号

1、RIP定义

中文版：

英文版：

概括：

（RIP）矩阵满足2K阶RIP保证了能够把任意一个K稀疏信号θK映射为唯一的y，也就是说要想通过压缩观测y恢复K稀疏信号θK，必须保证传感矩阵满足2K阶RIP，满足2K阶RIP的矩阵任意2K列线性无关。

边界解释：

上述定义中不等式边界关于1对称，其实这只是表示的方便而已，实际中可以考虑任意边界值。

2、RIP理解

理解1：能量说

向量的2范数的平方就是信号的能量，换成常见的公式：

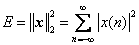
RIP不等式：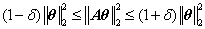

这里的实际上是，即输出信号的能量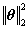，即输入信号的能量（稀疏变换x=Ψθ为正交变换，而正交变换保持能量不变，即信号理论中的Parseval定理）。

解释1：

解释2：

RIP其实可以看成刻画一个矩阵和标准正交阵的相似程度。其对于向量做变换后的 L2 能量（范数平方）相较于原向量的能量的变化不超过RIP。RIP对于Stability 的分析非常有效。RIP 是由Candes 和Tao 提出来的，可以看他们的提出这个概念的文章: Decoding by LinearProgramming。

其实取极限当δ=0时（RIP要求0<δ<1），RIP的不等式实际上表示的是观测所得向量y的能量等于信号x的能量，在线性代数中所讲的正交变换也具有这种性质，也称为等距变换（把信号将为二维或三维时2范数的平方可形象的理解为到原点的距离），当然这里的变换因为传感矩阵A不可能是正交矩阵（不是方阵），但当极限δ=0时也能保持能量相等（也可以称为等距吧），而RIP要求0<δ<1，所以不可能等距，所以就称为有限等距性质吧。

理解2：唯一映射说

在前一篇介绍spark常数的时候，已经提到了唯一映射说这一点，可以了解一下：http://www.cnblogs.com/AndyJee/p/5083726.html

RIP性质（有限等距性质）保证了感知矩阵不会把两个不同的K稀疏信号映射到同一个集合中（保证原空间到稀疏空间的一一映射关系），要求从感知矩阵中抽取的每2K个列向量构成的矩阵是非奇异的。

当δ2s<1时可以保证零范数问题有唯一的稀疏解，而当δ2s<sqrt(2)-1时则可以保证零范数和1范数等价（零范数求解为NP-hard问题，在此前提下将其转化为1范数求最优化问题，这时是个凸优化问题）

3、RIP补充

上面我们谈到的都是感知矩阵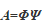，而实际中我们常常使用的是测量矩阵，那么怎么样才能让测量矩阵满足RIP要求呢？

前面解释中的能量说提到"RIP其实可以看成刻画一个矩阵和标准正交阵的相似程度"，如。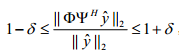

那么对于测量矩阵而言，需要满足的性质就是尽量保证其基向量与稀疏表示的基不相关，这个对于RIP来说比较通俗的理解，在实际中，有些矩阵如高斯随机矩阵、二值随机矩阵、局部傅里叶矩阵、局部哈达玛矩阵等都能够以很大的概率满足RIP。

关于矩阵中任意2K列都不相关的解释：

如果矩阵有2K列线性相关，则对于某一个2K稀疏的信号必然会有Aθ2K=0，又因为一个2K稀疏的信号可以写成两个K稀疏的信号相减（把2K稀疏信号的2K个非零项分成两部分，每部分分别包含K个非零项，其余部分填零长度与原2K稀疏信号保持不变，即得到了两个K稀疏信号，其中的一个K稀疏信号中的K个非零项乘负一，另一部分减这一部分必然等于2K稀疏信号），因此有A(θK1－θK2)=0，即AθK1=AθK2，也就是说对于两个不同的K稀疏信号θK1和θK2，压缩观测后得到了同一个y，即不能保证唯一映射，所以矩阵不能有2K列线性相关，否则将不能保证唯一映射。

4、参考文章

http://blog.csdn.net/jbb0523/article/details/44565647