Pick定理、欧拉公式和圆的反演

Pick定理、欧拉公式和圆的反演

Tags：高级算法

---

Pick定理

内容

定点都是整点的多边形，内部整点数为\(innod\)，边界整点数\(ednod\),\(S=innod+\frac{ednod}{2}-1\)

证明

把每个整点近似地看成一个圆，那么多边形内部的整点所代表的圆全部被算入
多边形边界上的圆被算了一半
顶点上被算了\(\sum 半圆-外角\)，外角和360度，于是\(-1\)

应用

POJ2954 求格点三角形内部点数

欧拉公式

内容

\[V-E+F=2\]
\(V:vertex\) 顶点
\(E:edge\) 边
\(F:Flat\) 面

适用于所有多变形（无论维度）

例如一个长方形：\(4\)个点\(4\)条边，两个面：里面和外面

应用

\(n\)个点做三维凸包，求增量构造法复杂度。

假设\(n\)个点都在凸包上，那么\(V=n\)，每个面有三条边，每条边被算了两次，即\(2E=3F\)
通过上面的公式可以得到\(F=2n-4,E=3n-6\)。
增量构造法的复杂度是面数×点数，所以是\(\cal O(n^2)\)级别

圆的反演变换

内容

反演中心为\(O\)，反演半径为\(R\)，若经过\(O\)的直线经过\(P,P'\)，且\(OP*OP'=R^2\)，则称\(P\)、\(P'\)关于\(O\)互为反演

性质

• 1.一根过\(O\)的直线的反形是本身
• 2.一根不过\(O\)的直线的反形是一个过\(O\)的圆
• 3.一个过\(O\)的圆的反形是一根不过\(O\)的直线
• 4.一个不过\(O\)的圆的反形是一个和该圆关于\(O\)位似的圆

下面这张图可以粗略解释一下有这么个东西：两种不同颜色的三角形相似，可以证出\(CD\)关于\(E\)的反形为圆

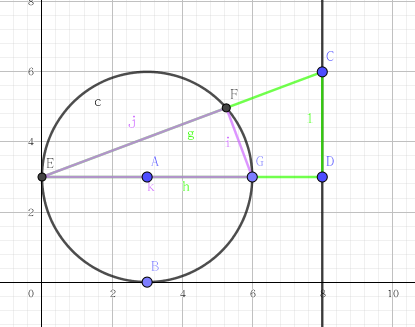
• 5.反演不改变相切关系

应用

1、求平面内与原点四点共圆的三元组个数

Problem Provider：自为风月马前卒
对所有点反演后求三点共线的三元组即可

2、求经过P点并与两给定相离圆外切的圆

参考博客：ACdreamer反演教程、水郁图文、cdsszjj题解、教你尺规画图
Problem Provider：HDU4773 Problem of Apollonius
先将两相离圆关于P反演，然后做反形的公切线，反演回来成为公切圆

TBC...