Demo003 最大连续子数组问题（《算法导论》4.1-5）

---

问题

问题描述

 给定n个整数（可能为负数）组成的数组，要求一个数组连续下标和的最大值，数组的元素可正、可负、可为零。

 数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。求所有子数组的和的最大值。

 例如输入的数组为 -2 , 11 , -4 , 13 , -5 , -2时，最大的子数组为11,-4,13，因此最大子数组的和为20。

解题思路

 很容易理解，当我们加上一个正数时，和会增加；当我们加上一个负数时，和会减少。如果当前得到的和是个负数，那么这个和在接下来的累加中应该抛弃并重新清零，不然的话这个负数将会减少接下来的和。

 从其实点i到目标点j，从第一个正数开始截取尽量长的一段数组，从第一个正数起的最大子数组即为当前数组的最大子数组，若数组和为负，则不可能作为更长数组最大子数组的组成部分（因为还不如从零直接取第一个正数），因此清零数组和并从接下来的第一个正数重新截取。

 在此过程中，我们通常说“一个最大子数组”而不是“最大子数组”，因为可能有多个子数组达到最大和。

 只有当数组中包含负数时，最大子数组问题才有意义。如果所有数组元素都是非负的，最大子数组问题没有任何难度，因为整个数组的和肯定是最大的。

---

思路1：暴力枚举法

1.思路分析

 先找出从第1个元素开始的最大子数组(先从第一个元素开始向后累加，每次累加后与之前的和比较，保留最大值)，

 而后再从第2个元素开始找出从第2个元素开始的最大子数组，依次类推，比较得出最大的子数组。

 记：最大子数组的和为maxium（起点为 low ，终点为 high），初始值为-INF;

 正在扫描的子数组的和为sum（起点为 i ，终点为 j ），初始值为0。

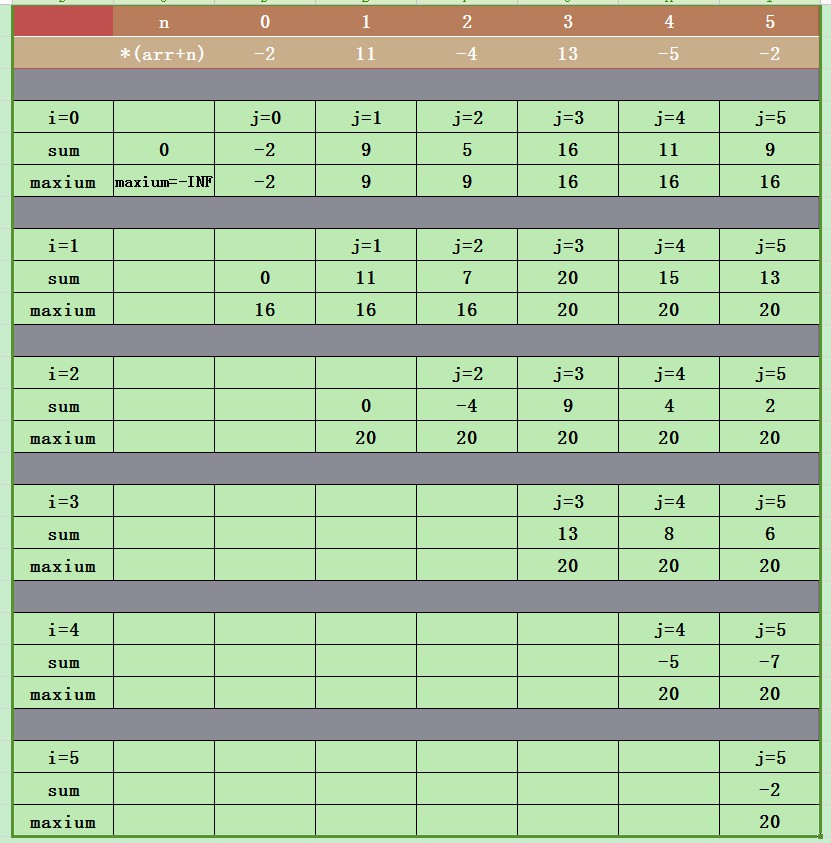
2.复杂度

 遍历所有可能的sum[i, …, j]，时间复杂度为O(n^2)，空间复杂度O(1)。

3.伪代码

int maxSubArray(int *arr,int n,int &low,int &high)
{
    int maxium = -INF;       //maxium 最大子数组的和 初始值为-INF
    for i=0 to n-1 do
        sum = 0;          //正在扫描的子数组的和 初始值为0
        for j=i to n-1 do
            sum += arr[j];
            if sum>maxium do      //将 maxium 更新为 sum
                maxium = sum;
                low=i;
                high=j;
    return maxium;
}  

4.analysis in C

int maxSubArray(int *arr,int n,int &low,int &high)
{
    int maxium=-INF;
    for(int i=0;i<=n-1;i++){
        int sum=0;
        for(int j=i;j<=n-1;j++)
        {
            sum += arr[j];
            if(sum > maxium)
            {
                maxium = sum;
                low = i;
                high = j;
            }
        }
    }
    return maxium;
}

5.analysis in java

package com.ryanjie.task03;

/**
 * @program: Demo003
 * @description: return MaxSubArray
 * @author: Ryanjie
 * @create: 2018-04-01 19:42
 **/

public class MaxSubArray1{

    public int Method1(int[] arr){
        int maxium = arr[0];
        int sum = 0;;
        for(int i = 0;i < arr.length;i++){
            for(int j = i;j < arr.length;j++){
                for(int k = i;k <= j;k++){
                    sum += arr[k];
                }
                if(sum > maxium)
                    maxium = sum;
                sum = 0;             //完成一个子序列求和后，重新赋值为0
            }
        }
        return maxium;
    }

    public static void main(String[] args){
        MaxSubArray1 test = new MaxSubArray1();
        int[] A = {-2 , 11 , -4 , 13 , -5 , -2};
        System.out.println("蛮力法求解数组A的最大连续子数组和为："+test.Method1(A));
    }
}

测试结果：

蛮力法求解数组A的最大连续子数组和为：20

---

思路2：分治法

 《算法导论》分治法---分而治之：想要为一个问题找出分治的解法，关键在于怎么分和分了之后怎么找出一个时间复杂度可以接受的算法 。

1.思路分析

 我们把数组A[1..n]划分为两个规模尽量相等的子数组：arr[1..n/2] 和 A[n/2+1..n]，也就是说,找到数组的中间位置mid(n/2).

 最大的子数组A[low..high]只可能出现在三种情况（如图2所示）：

• 完全位于子数组 A[ 1...mid]中 ;
• 完全位于子数组 A[ mid+1...n ]中 ;
• 跨越了中点,在子数组 A[ i..mid..j ]中 ;

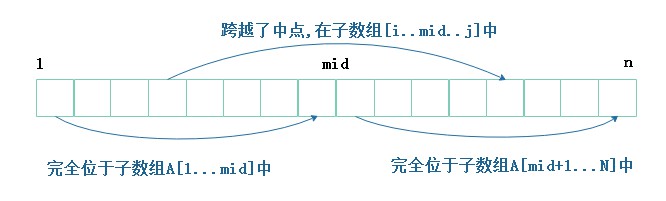
 前面两种情况的解法和整体的解法一样，用递归解决，主要看第三个情况。

 如图3所示，任何跨越中点的子数组一定包含左半边数组的最大后缀和右半边数组的最大前缀，都由两个子数组A[i..mid]和A[mid+1..j]组成，其中 1 <= i <= mid 且 mid+1 <= j <= n 。因此，我们只需找出形如A[i..mid]和A[mid+1..j]的最大子数组，然后将其合并即可。

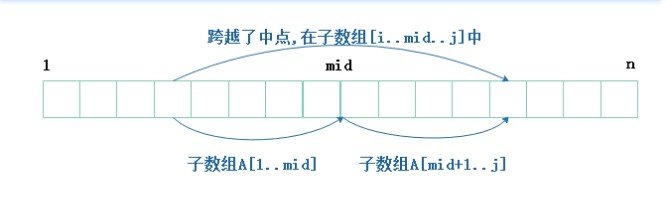
2.复杂度：时间复杂度O(nlogn)，空间复杂度O(1)

3.伪代码

int maxSubArray(int *arr,int low,int high)
{
    left_sum = -INF;
    right_sum = -INF;
    max_left = -1;
    max_right = -1;

    sum = 0;    //from mid to left search left_sum
    for i=mid downto low do
        sum += arr[i];
        if sum > left_sum do
            left_sum = sum;
            max_left = i;

    sum = 0;    //from mid to right search right_sum
    for i=mid+1 to high do
        sum += arr[j];
        if sum > right_sum do
            right_sum = sum;
            max_right = j;

    return (left_sum + right_sum);
}

4.analysis in C：

int maxSubArray(int *arr,int low,int right)
{
    int left_sum = -INF;
    int right_sum = -INF;

    int max_left = -1,;
    int max_right = -1;

    int sum = 0;      //from mid to left search left_sum
    for (int i = mid; i >= low; i --) {
        sum += arr[i];
        if (sum > left_sum) {
            left_sum = sum;
            max_left = i;
        }
    }
    sum = 0;      //from mid to right search right_sum
    for (int j = mid + 1; j <= high; j ++) {
        sum += arr[j];
        if (sum > right_sum) {
            right_sum = sum;
            max_right = j;
        }
    }
    return (left_sum + right_sum);
}

---

思路3：动态规划

1.思路分析

 令cursum(i)表示数组下标以i为起点的最大连续下标最大的和，而maxsum(i)表示前i个元素的最大子数组之和。那么我们就可以推出下一个maxsum(i+1)应该为cursum(i+1)和maxsum(i)中选取一个最大值。递推式为：
 cursum(i) = max{A[i],cursum(i-1)+A[i]};
 maxsum(i) = max{maxsum(i-1),cursum(i+1)};
 转移方程为：
 f_i=max(f_i-1+a_i,a_i)

2.复杂度：时间复杂度O(n)

3.伪代码

int maxSubArray(int *A,int n)
{
    cursum = A[0];
    maxsum = A[0];
    for i=1 to n-1 do
 /*当我们加上一个正数时，和会增加；当我们加上一个负数时，和会减少。如果当前得到的和是个负数，那么这个和在接下来的累加中应该抛弃并重新清零，不然的话这个负数将会减少接下来的和。*/
        if cursum<0 do
            cursum = 0;
        cursum += A[i];
        if cursum>maxsum do
            maxsum = cursum;
    return maxsum;
}  

4.analysis in java

package com.ryanjie.task03;

/**
 * @program: Demo003
 * @description: return MaxSubArray
 * @author: Ryanjie
 * @create: 2018-04-01 19:50
 **/
public class MaxSubArray2 {
     int Method2(int[] A){
        int cursum = A[0];
        int maxsum = cursum;
        for(int i = 0;i < A.length;i++){
            if(cursum >= 0)
                cursum += A[i];
            else
                cursum = A[i];
            if(cursum > maxsum)
                maxsum = cursum;
        }
        return maxsum;
    }

    public static void main(String[] args){
        MaxSubArray2 test = new MaxSubArray2();
        int[] A = {-2 , 11 , -4 , 13 , -5 , -2};
        System.out.println("动态规划法求解数组A的最大连续子数组和为："+test.Method2(A));
    }
}

测试结果：

动态规划法求解数组A的最大连续子数组和为：20

测试

从语句覆盖、判定覆盖、条件覆盖、判定/条件覆盖、条件组合覆盖五个覆盖标准中选取条件组合覆盖进行测试，测试代码如下：

package com.ryanjie.task03; 

import org.junit.Test;
import static org.junit.Assert.*;

/**
* MaxSubArray2 Tester.
*
* @author Ryanjie
* @since <pre>04/01/2018</pre>
* @version 1.0
*/
public class MaxSubArray2Test {

    @Test
    public void testManualAllPositiveArray() {
        int arr[] = new int[] {1, 2, 3, 4, 5, 6};
        assertEquals(22, new MaxSubArray2().Method2(arr));
    }

    @Test
    public void testManualAllPositiveArray1() {
        int[] arr = new int[]{0, 0, 18, 0, 0, -6};
        assertEquals(18, new MaxSubArray2().Method2(arr));
    }

    @Test
    public void testManualAllPositiveArray2() {
        int[] arr = new int[] {-2, 11, -4, 13, -5, -2};
        assertEquals(20, new MaxSubArray2().Method2(arr));
    }

    @Test
    public void testManualAllPositiveArray3() {
        int[] arr = new int[] {-2 , 11 , -4 , 13 , -5 , -2};
        assertEquals(20, new MaxSubArray2().Method2(arr));
    }

}

测试截图：

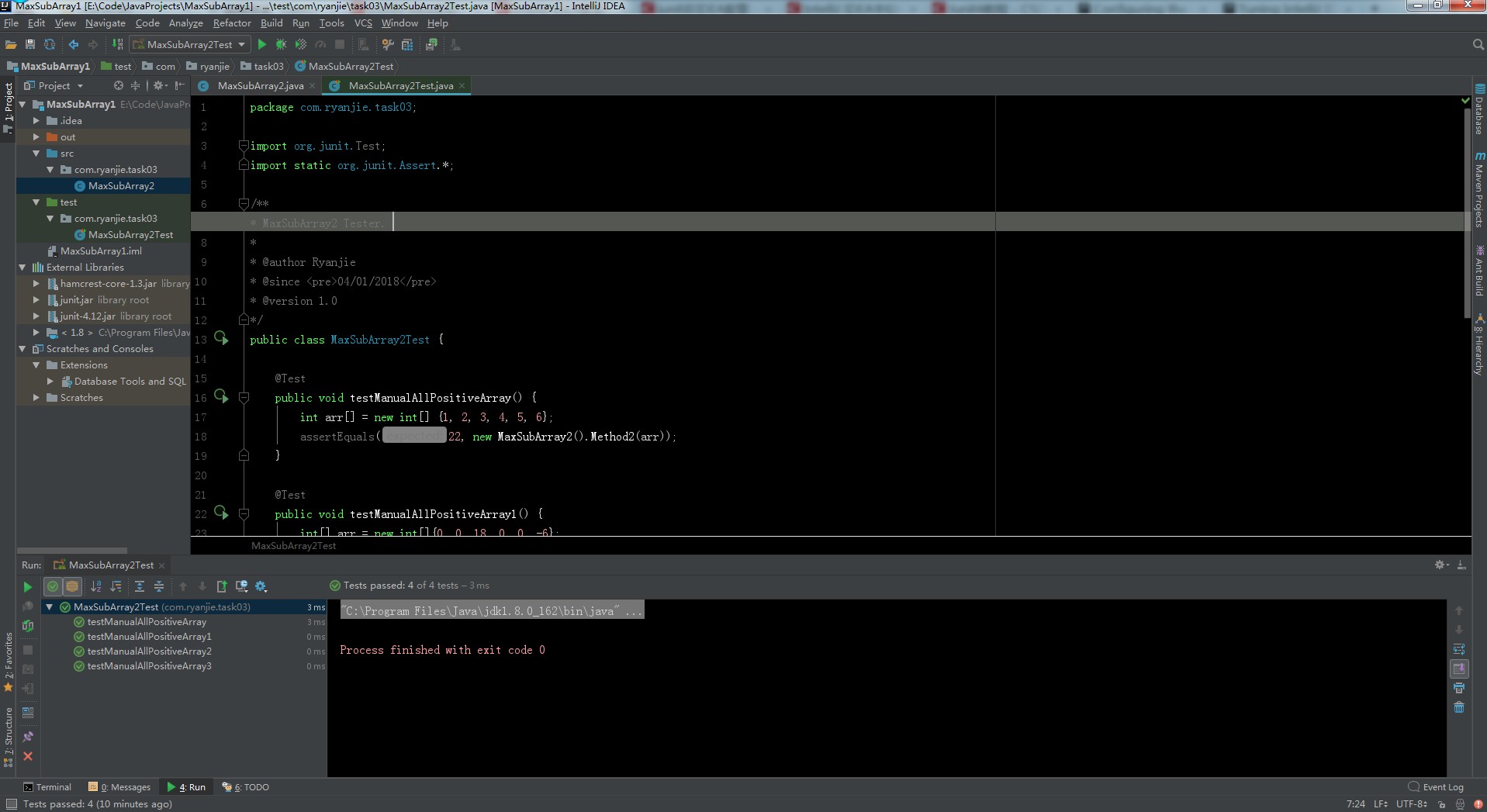
coding代码：Task03