Bzoj2694/Bzoj4659:莫比乌斯反演

Bzoj2694/Bzoj4659:莫比乌斯反演

先上题面:

首先看到这数据范围显然是反演了，然而第三个限制条件十分不可做。于是我们暂且无视他，大不了补集转化算完再减是吧。

于是我们有: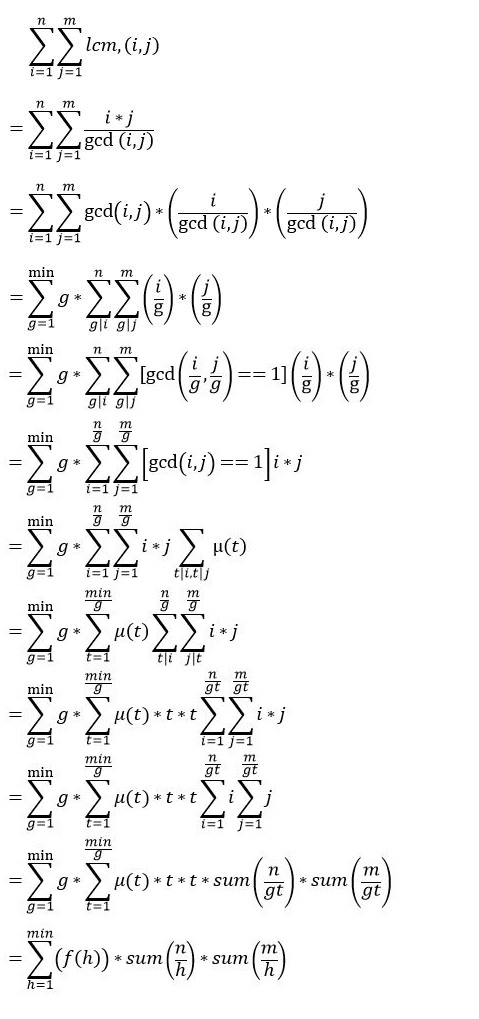

这里我们定义: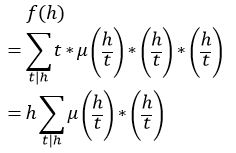

于是这个东西我们可以nlogn筛的说。
也就是说，我们求出f的前缀和后，就可以O(sqrt(n)+sqrt(m))分块计算了。
然而需要减去的东西怎么办呢？
反演题最难的不是推公式，而是你推出了公式却不知道是否可做。
仔细观察以上两个式子，原式中的g(也就是上式中的t)，不就是我们枚举的gcd吗?
题面要求两个数不同时含某个平方因数，也就是他们的gcd不同时含某个平方因数。
那不就是我们原式中的g(上式中的t)不含平方因数吗?
而一个数x含平方因数，会有什么性质呢?μ(x)=0!
所以我们先枚举t，判断其μ值非0，然后去枚举h/t，更新f(h)即可。
这题取模2^30，我们直接用int自然溢出就好了。
(为什么?因为这样加减乘显然是对的，然而除法，只有在计算sum的时候会除二，这样我们会损失一位的精度。而int的正数精度为取模2^31的，损失一位后正好够用，所以我们可以这样做。理论上取模2^31我们也可以用unsigned int做，然而取模2^32就必须long long了。以上内容纯属口胡，如果因此wa了别打我就是了QAQ……)

代码:
(一开始sieve里面开的数组没加static wa了一次，身败名裂)

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define lli long long int
 #define debug cout
 using namespace std;
 const int maxn=4e6+1e2,lim=4e6;
 const int mod =  << ;

 int mu[maxn],f[maxn];

 inline void sieve() {
     static int prime[maxn],cnt;
     static bool vis[maxn];
     mu[] = ;
     for(int i=;i<=lim;i++) {
         if( !vis[i] ) prime[++cnt] = i , mu[i] = -;
         for(int j=;j<=cnt&&(lli)i*prime[j]<=lim;j++) {
             const int tar = i * prime[j];
             vis[tar] = ;
             if( ! ( i % prime[j] ) ) break;
             mu[tar] = -mu[i];
         }
     }
     for(int i=;i<=lim;i++) if( mu[i] ) {
         for(int j=;(lli)i*j<=lim;j++) f[i*j] += j * mu[j];
     }
     for(int i=;i<=lim;i++) f[i] *= i , f[i] += f[i-];
 }
 inline int sum(int x) {
     return x * ( x +  ) >> ;
 }
 inline int calc(int n,int m) {
     if( n > m ) swap(n,m);
     int ret = ;
     for(int l=,r;l<=n;l=r+) {
         r = min( n / ( n / l ) , m / ( m / l ) );
         ret += ( f[r] - f[l-] ) * sum(n/l) * sum(m/l);
     }
     return ret;
 }

 int main() {
     static int T,a,b;
     static lli ans;
     scanf("%d",&T) , sieve();
     while(T--) {
         scanf("%d%d",&a,&b) , ans = calc(a,b);
         ans = ( ans % mod + mod ) % mod;
         printf("%lld\n",ans);
     }
     return ;
 }