hiho 1182 : 欧拉路·三

1182 : 欧拉路·三

这时题目中给的提示：

小Ho：是这样的，每次转动一个区域不是相当于原来数字去掉最左边一位，并在最后加上1或者0么。

于是我考虑对于"XYYY"，它转动之后可以变成"YYY0"或者"YYY1"。我就将所有的数字0~2^N-1看作2^N个点，连接所有的("XYYY","YYY0"),("XYYY","YYY1")。

比如当N=3时，我得到了这样一个图：

我要做的就是找一条路径，从一个点出发，走过所有的点后，再回到起点。但是我发现好像很难的样子。

小Hi：那当然了。你这样构造出来的路径叫做哈密顿回路，不是那么容易可以求解的。

小Ho：哎？？那我应该怎么做。

小Hi：其实你的想法是没问题的，但是需要进行一下变换。在你的构图中我们是用点来表示数字，所以需要经过每一个点。如果我们用边来表示每一个数字呢？

小Ho：怎么用边表示数字？

小Hi：其实也很简单，比如说数字"10011"，分别删掉它第一个数字和最后一个数字，得到"1001","0011"。然后我们连接一条从"1001"到"0011"的有向边，表示数字"10011"。则我们可以得到构图的方法：

对于N，我们构造一个包含2^(N-1)个点和2^N条边的图，点的编号从0到2^(N-1)-1。编号为i的点表示数字i。对于任意两个点，如果点i,点j满足点i的后n-2个数字和点j的前n-2个数字相同，则我们连接有向边(i,j)。而边(i,j)表示了数字((i << 1)+(j & 1))。比如对于N=3的时候，我们可以得到：

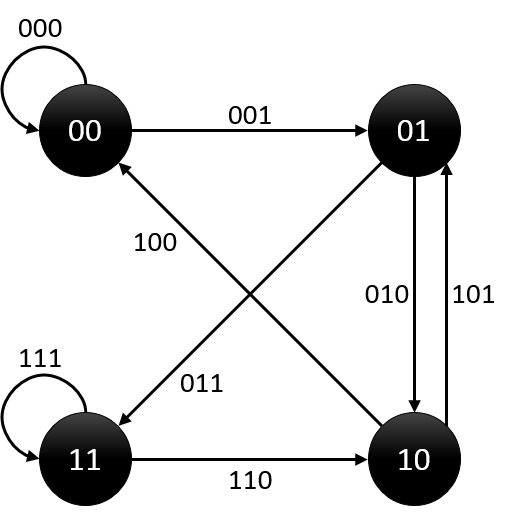
可以很容易证明对于任意不同边(i,j)，其表示的数字一定不同。

小Ho：这样构图话，只要找到一条欧拉回路就可以了。但是一定会有欧拉回路么？

小Hi：当然能了，对于有向图，其存在欧拉路的条件是，至多有两个点的入度不等于出度，且这两个点满足：其中一个点入度比出度多1，另一个点出度比入度多1。

若所有点的入度都等于出度，则一定存在欧拉回路。这可以通过和无向图欧拉路同样的方法进行构造证明。

而我们构造的图，由构造方法可以知道对于任意一个点，其入度一定为2，出度一定为2。所以它必定存在欧拉回路。

在有向图中找欧拉路的方法，也仍然可以使用Fleury算法。写成伪代码的话：

DFS(u):
	While (以u为起点，且未被删除的边e(u,v))
		删除边e(u,v)
		DFS(v)
	End
	PathSize ← PathSize + 1
	Path[ PathSize ] ← u
		

但是，有一点要注意，在使用Fleury算法计算有向图的欧拉路时，我们需要将path[]倒序输出才能得到正确的路径。

小Ho：那找到欧拉回路之后呢？

小Hi：找到欧拉回路之后只要对该条欧拉回路进行拼接就可以得到我们目标的圆盘状态了。

小Ho：好，我大概明白了。我这就来试试！

题目分析：

提示中说的很清楚： 好好看看上面的讲解。 很聪明的地方是把图一变成了图二（图二也就是用边表示n位二进制可以表示的所有数。n=3时， 是0~7），节省了空间。  如果存在一个欧拉回路， 也就是存在一条路径每条边都走过并且只走一遍， 最后回到原点， 那么就可以说这个转盘可以表示n位二进制可以表示的所有数。用fleury求路径， 边球路径边记录，fleury不明白点这里。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<vector>
using namespace std;

int n, top, key, final[], ans[];
vector<int> vec[];

void init()//初始化把所有边标记出来
{
    for(int i = ; i < ( << n - ); i++)
    {
        int j = i << ; // 点i向左移一位
        int t =  << (n - );
        j = j & (t - );//舍去第一位
        vec[i].push_back(j); //最后一位加0
        vec[i].push_back(j+); //最后一位添1
    }
}
void dfs(int x)
{
    ans[++top] = x;
    if(vec[x].size() > )
    {
        int tmp = vec[x][];
        vec[x].erase(vec[x].begin()+);//要记得删除便利过的点
        dfs(tmp);
    }
}
void fleury(int x)
{
    top = ;
    ans[top] = x;
    while(top > )
    {
        if(vec[ans[top]].size() > )//如果可扩展， 则dfs可扩展的哪条路线
        {
            top--;
            dfs(ans[top+]);
        }
        else//该点x没有其他的边可以先走了（即不可扩展）， 那么就用final记录下来
        {
            final[++key] = ans[top];
            //ans只是记录路径的中间记录， 可能会变， 一定要用final做最后的记录
            top--;
        }
    }
}
int main()
{
    while(scanf("%d", &n) != EOF)
    {
        for(int i = ; i < ( << n); i++) vec[i].clear();
        init();
        key = ;
        fleury();
        for(int i = ; i <= ( << n); i++)//将路径的每个值的最后一个二进制的值求出即可
        {
            int tmp = final[i] & ;
            printf("%d", tmp);
        }
        cout << endl;
    }
    return ;
}