POJ 1410 Intersection （线段和矩形相交）

题目：

Description

You are to write a program that has to decide whether a given line segment intersects a given rectangle.

An example: 
line: start point: (4,9) 
end point: (11,2) 
rectangle: left-top: (1,5) 
right-bottom: (7,1)

 
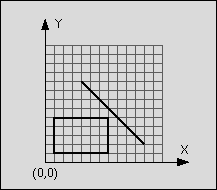
Figure 1: Line segment does not intersect rectangle

The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.

Input

The input consists of n test cases. The first line of the input file contains the number n. Each following line contains one test case of the format: 
xstart ystart xend yend xleft ytop xright ybottom

where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.

Output

For each test case in the input file, the output file should contain a line consisting either of the letter "T" if the line segment intersects the rectangle or the letter "F" if the line segment does not intersect the rectangle.

Sample Input

1
4 9 11 2 1 5 7 1

Sample Output

F

---

题意：给出一条线段和一个矩形 判断两者是否相交
思路：就直接暴力判断 但是要考虑一些边界情况 曾经在判断线段是否在矩形内的时候莫名其妙wa 

---

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>

using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int inf=0x3f3f3f3f;
const double eps=1e-;
int n;
double x,y,xx,yy,tx,ty,txx,tyy;

int dcmp(double x){
    if(fabs(x)<eps) return ;
    if(x<) return -;
    else return ;
}

struct Point{
    double x,y;
    Point(){}
    Point(double _x,double _y){
        x=_x,y=_y;
    }
    Point operator + (const Point &b) const{
        return Point(x+b.x,y+b.y);
    }
    Point operator - (const Point &b) const{
        return Point(x-b.x,y-b.y);
    }
    double operator * (const Point &b) const{
        return x*b.x+y*b.y;
    }
    double operator ^ (const Point &b) const{
        return x*b.y-y*b.x;
    }
};

struct Line{
    Point s,e;
    Line(){}
    Line(Point _s,Point _e){
        s=_s,e=_e;
    }
};

bool inter(Line l1,Line l2){
    return
        max(l1.s.x,l1.e.x)>=min(l2.s.x,l2.e.x) &&
        max(l2.s.x,l2.e.x)>=min(l1.s.x,l1.e.x) &&
        max(l1.s.y,l1.e.y)>=min(l2.s.y,l2.e.y) &&
        max(l2.s.y,l2.e.y)>=min(l1.s.y,l1.e.y) &&
        dcmp((l2.s-l1.e)^(l1.s-l1.e))*dcmp((l2.e-l1.e)^(l1.s-l1.e))<= &&
        dcmp((l1.s-l2.e)^(l2.s-l2.e))*dcmp((l1.e-l2.e)^(l2.s-l2.e))<=;
}

int main(){
    scanf("%d",&n);
    while(n--){
        scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&x,&y,&xx,&yy,&tx,&ty,&txx,&tyy);
        double xl=min(tx,txx);
        double xr=max(tx,txx);
        double ydown=min(ty,tyy);
        double yup=max(ty,tyy);
        Line line=Line(Point(x,y),Point(xx,yy));
        Line line1=Line(Point(tx,ty),Point(tx,tyy));
        Line line2=Line(Point(tx,ty),Point(txx,ty));
        Line line3=Line(Point(txx,ty),Point(txx,tyy));
        Line line4=Line(Point(txx,tyy),Point(tx,tyy));
        if(inter(line,line1) || inter(line,line2) || inter(line,line3) || inter(line,line4) || (max(x,xx)<xr && max(y,yy)<yup && min(x,xx)>xl && min(y,yy)>ydown)) printf("T\n");
        else printf("F\n");
    }
    return ;
}