HDU4453--Looploop (Splay伸展树)

Looploop

XXX gets a new toy named Looploop. The toy has N elements arranged in a loop, an arrow pointing to one of the elements, and two preset parameters k1 and k2. Every element has a number on it.

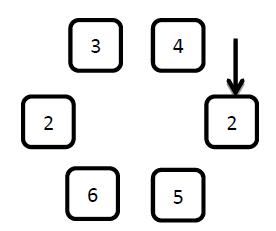
The figure above shows a Looploop of 6 elments. Let's assuming the preset parameter k1 is 3, and k2 is 4.
XXX can do six operations with the toy.

1: add x 
Starting from the arrow pointed element, add x to the number on the clockwise first k2 elements.

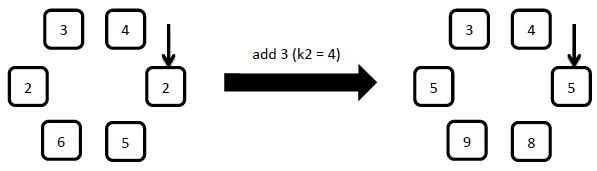
2: reverse
Starting from the arrow pointed element, reverse the first k1 clockwise elements.

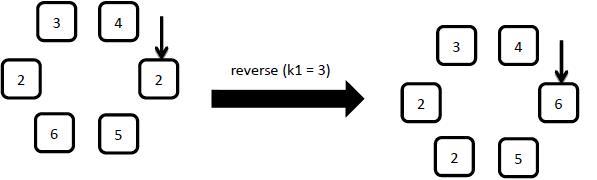
3: insert x 
Insert a new element with number x to the right (along clockwise) of the arrow pointed element.

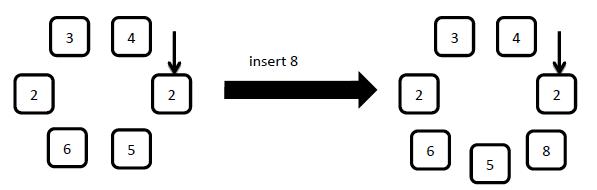
4: delete 
Delete the element the arrow pointed and then move the arrow to the right element.

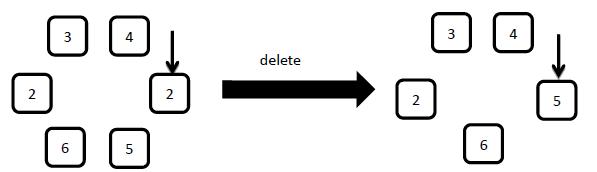
5: move x 
x can only be 1 or 2. If x = 1 , move the arrow to the left(along the counterclockwise) element, if x = 2 move the arrow to the right element.

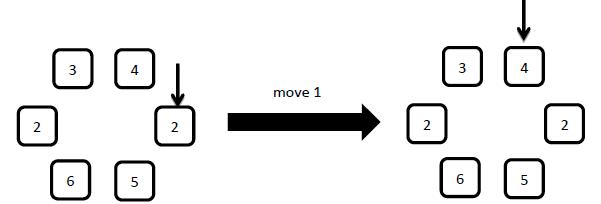
6: query
Output the number on the arrow pointed element in one line.

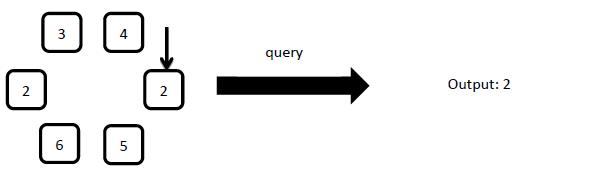
XXX wants to give answers to every query in a serial of operations.

 

Input

There are multiple test cases.
For each test case the first line contains N,M,k1,k2(2≤k1<k2≤N≤10⁵, M≤10⁵) indicating the initial number of elements, the total number of operations XXX will do and the two preset parameters of the toy. 
Second line contains N integers ai(-10⁴≤ai≤10⁴) representing the N numbers on the elements in Looploop along clockwise direction. The arrow points to first element in input at the beginning. 
Then m lines follow, each line contains one of the six operations described above.
It is guaranteed that the "x" in the "add","insert" and "move" operations is always integer and its absolute value ≤104. The number of elements will never be less than N during the operations. 
The input ends with a line of 0 0 0 0.

Output

For each test case, output case number in the first line(formatted as the sample output). Then for each query in the case, output the number on the arrow pointed element in a single line.

 

Sample Input

5 1 2 4
3 4 5 6 7
query
5 13 2 4
1 2 3 4 5
move 2
query
insert 8
reverse
query
add 2
query
move 1
query
move 1
query
delete
query
0 0 0 0

 

Sample Output

Case #1:

3

Case #2:

2

8

10

1

5

1

2012 Asia Hangzhou Regional Contest

题意很简单，就像题目中 图片中描述的一样。Splay大法好啊。

 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <algorithm>
 using namespace std;
 const int inf = 0x3f3f3f3f;
 const int maxn = ;
 int pre[maxn],ch[maxn][],key[maxn],addv[maxn],rev[maxn],siz[maxn];
 int tot1,tot2,root,s[maxn];  //s为内存池
 int a[maxn],n,m,k1,k2;
 void update_add(int r,int val)
 {
     if (!r)
         return;
     key[r] += val;
     addv[r] += val;
 }
 void update_rev(int r)
 {
     if (!r)
         return;
     swap(ch[r][],ch[r][]);
     rev[r] ^= ;
 }
 void push_down(int r)
 {
     if (rev[r])
     {
         update_rev(ch[r][]);
         update_rev(ch[r][]);
         rev[r] = ;
     }
     if (addv[r])
     {
         update_add(ch[r][],addv[r]);
         update_add(ch[r][],addv[r]);
         addv[r] = ;
     }
 }
 void push_up(int r)
 {
     siz[r] = siz[ch[r][]] + siz[ch[r][]] + ;
 }
 void NewNode (int &r,int father,int k)
 {
     if (tot2)
         r = s[tot2--];
     else
         r = ++tot1;
     pre[r] = father;
     siz[r] = ;
     rev[r] = ;
     addv[r] = ;
     ch[r][] = ch[r][] = ;
     key[r] = k;
 }
 void build(int &x,int l,int r,int father)
 {
     if (l > r)
         return ;
     int mid = (l + r) >> ;
     NewNode(x,father,a[mid]);
     build(ch[x][],l,mid-,x);
     build(ch[x][],mid+,r,x);
     push_up(x);
 }
 void init()
 {
     tot1 = tot2 = root = ;
     for (int i = ; i <= n; i++)
         scanf ("%d",a+i);
     NewNode(root,,inf);
     NewNode(ch[root][],root,inf);
     build(ch[ch[root][]][],,n,ch[root][]);
     push_up(root);
     push_up(ch[root][]);
 }
 void Rotate(int r,int kind)
 {
     int y = pre[r];
     push_down(y);
     push_down(r);
     ch[y][!kind] = ch[r][kind];
     pre[ch[r][kind]] = y;
     if (pre[y])
         ch[pre[y]][ch[pre[y]][] == y] = r;
     ch[r][kind] = y;
     pre[r] = pre[y];
     pre[y] = r;
     push_up(y);
 }

 void Splay(int r,int goal)
 {
     push_down(r);
     while (pre[r] != goal)
     {
         if (pre[pre[r]] == goal)
         {
             push_down(pre[r]);
             push_down(r);
             Rotate(r,ch[pre[r]][] == r);
         }
         else
         {
             int y = pre[r];
             int kind = (ch[pre[y]][] == y);
             push_down(pre[y]);
             push_down(y);
             push_down(r);
             if (ch[y][kind] == r)
             {
                 Rotate(y,!kind);
                 Rotate(r,!kind);
             }
             else
             {
                 Rotate(r,kind);
                 Rotate(r,!kind);
             }
         }
     }
     push_up(r);
     if (goal == )
         root = r;
 }
 int Get_kth(int r,int k)
 {
     push_down(r);
     int t = siz[ch[r][]] + ;
     if (t == k)
         return r;
     if (t > k)
         return Get_kth(ch[r][],k);
     else
         return Get_kth(ch[r][],k-t);
 }
 void ADD(int x)
 {
     Splay (Get_kth(root,),);
     Splay(Get_kth(root,k2+),root);
     update_add(ch[ch[root][]][],x);
     push_up(ch[root][]);
     push_up(root);
 }
 void Reverse(int u,int v)
 {
     Splay(Get_kth(root,u),);
     Splay(Get_kth(root,v+),root);
     update_rev(ch[ch[root][]][]);
     push_up(ch[root][]);
     push_up(root);
 }
 void Insert(int x)
 {
     Splay(Get_kth(root,),);
     Splay(Get_kth(root,),root);
     NewNode(ch[ch[root][]][],ch[root][],x);
     push_up(ch[root][]);
     push_up(root);
 }
 void eraser(int r)
 {
     if (!r)
         return;
     s[++tot2] = r;
     eraser(ch[r][]);
     eraser(ch[r][]);
 }
 void Delete()
 {
     Splay(Get_kth(root,),);
     Splay(Get_kth(root,),root);
     eraser(ch[ch[root][]][]);
     pre[ch[ch[root][]][]] = ;
     ch[ch[root][]][] = ;
     push_up(ch[root][]);
     push_up(root);
 }
 void Move(int x)               //Move操作就是两个 区间reverse操作。
 {
     if (x == )
     {
         Reverse(,n);
         Reverse(,n);
     }
     if (x == )
     {
         Reverse(,n);
         Reverse(,n-);
     }
 }
 int query()
 {
     Splay(Get_kth(root,),);
     Splay(Get_kth(root,),root);
     return key[ch[ch[root][]][]];
 }
 int main(void)
 {
     #ifndef ONLINE_JUDGE
         freopen("in.txt","r",stdin);
     #endif
     int cas = ;
     while (~scanf ("%d%d%d%d",&n,&m,&k1,&k2))
     {
         if (n ==  && m ==  && k1 ==  && k2 == )
             break;
         printf("Case #%d:\n",cas++);
         init();
         for (int i = ; i < m; i++)
         {
             char op[];
             int x;
             scanf ("%s",op);
             if (op[] == 'a')
             {
                 scanf ("%d",&x);
                 ADD(x);
             }
             if (op[] == 'r')
                 Reverse(,k1);
             if (op[] == 'i')
             {
                 scanf ("%d",&x);
                 Insert(x);
                 n++;           // insert一个数  n自然加1
             }
             if (op[] == 'd')
             {
                 Delete();
                 n--;          //delete一个数 n减1
             }
             if (op[] == 'm')
             {
                 scanf ("%d",&x);
                 Move(x);
             }
             if (op[] == 'q')
                 printf("%d\n",query());
         }
     }
     return ;
 }