POJ - 3111 K Best 0-1分数规划 二分

K Best

Time Limit: 8000MS		Memory Limit: 65536K
Total Submissions: 12812		Accepted: 3290
Case Time Limit: 2000MS		Special Judge

Description

Demy has n jewels. Each of her jewels has some value v_i and weight w_i.

Since her husband John got broke after recent financial crises, Demy has decided to sell some jewels. She has decided that she would keep k best jewels for herself. She decided to keep such jewels that their specific value is as large as possible. That is, denote the specific value of some set of jewels S = {i₁, i₂, …, i_k} as

.

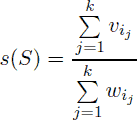Demy would like to select such k jewels that their specific value is maximal possible. Help her to do so.

Input

The first line of the input file contains n — the number of jewels Demy got, and k — the number of jewels she would like to keep (1 ≤ k ≤ n ≤ 100 000).

The following n lines contain two integer numbers each — v_i and w_i (0 ≤ v_i ≤ 10⁶, 1 ≤ w_i ≤ 10⁶, both the sum of all v_i and the sum of all w_i do not exceed 10⁷).

Output

Output k numbers — the numbers of jewels Demy must keep. If there are several solutions, output any one.

Sample Input

3 2
1 1
1 2
1 3

Sample Output

1 2

Source

Northeastern Europe 2005, Northern Subregion

题目链接 点击打开链接

题目大意：给你N个珠宝已经每个珠宝的价值和重量，取其中K个。问取哪几个珠宝使得sigma(v[i])/ sigma(w[i])最大。

思路：构造函数 sigma(t[i]) = sigma(v[i]) - sigma(w[i]) * x。 然后二分x值。   方法为0-1分数规划。

#include<stdio.h>
#include<algorithm>
using namespace std;

#define exp 1e-8
struct jew{
	int id;
	double y;
}num[1000005];
double v[1000005], w[1000005];
bool cmp(jew a, jew b)
{
	return a.y > b.y;
}

bool dis(double x, int n, int k)
{
	int i;
	double sum = 0;
	for (i = 0; i < n; i++)
	{
		num[i].y = v[i] - x*w[i];
		num[i].id = i + 1;
	}
	sort(num, num + n, cmp);
	for (i = 0; i < k; i++)
	{
		sum += num[i].y;
	}
	return sum >= 0;
}
int main()
{
	int n, k;
	while (~scanf("%d %d", &n, &k))
	{
		for (int i = 0; i < n; i++)
		{
			scanf("%lf %lf", &v[i], &w[i]);
		}
		double left = 0, right = 1e6;
		double mid;
		while (right - left>=exp)
		{
			mid = (left + right) / 2;
			if (dis(mid, n, k))
			{
				left = mid;
			}
			else
			{
				right = mid;
			}
		}
		for (int i = 0; i < k - 1; i++)
		{
			printf("%d ", num[i].id);
		}
		printf("%d\n", num[k - 1].id);
	}

	return 0;
}