单调队列优化O(N)建BST P1377 [TJOI2011]树的序

洛谷 P1377 [TJOI2011]树的序 (单调队列优化建BST

---

链接

题意分析

本题思路很简单，根据题意，我们利用所给的Bst生成序将Bst建立起来，然后输出该BST的先序遍历即可；

但，如果我们不加优化，建BST的时间复杂度在最劣情况下将达到O(n^2)，显然，在1e5的数据下是过不去的，所以我们考虑利用利用单调队列优化来建BST；

算法思路

BST建树本质上便是按照权值将新加入节点插入到对应的位置，该过程受插入顺序

影响

我们考虑可以将读入的生成序列的下标变成权值，本身权值变为下标

for(int i=1;i<=n;i++){
		x=read();
		a[x]=i;
	}

因为权值为1-n的序列，我们将该数组从1-n遍历，本质便是按权值从小到大遍历(如

果权值不是1-n的序列，将其离散化即可)

我们按该方式维护一个单调队列，当一个新数进队列后不在向前更新时，我们便将

该节点插到单调队列中它左侧节点的右子树中，原因很简单，该节点左侧的节点先

入队列，说明左侧权值一定比该节点小,故将该点插入到左侧节点的右子树上，假设

该节点进队列过程中压掉了节点，则将该节点插入到被它压掉的最后一个节点的左

子树上，我们用此方法便可以在O(n)的时间复杂度下建成一颗bst了，建树代码如下

	int tot=0;
	int pos=0;
	for(int i=1;i<=n;i++){
		tot=pos;
		while(pos&&a[q[pos]]>a[i]){
			pos--;
		}
		if(pos){
			r[q[pos]]=i;
		}
		if(pos<tot){
			l[i]=q[pos+1];
		}
		q[tot=++pos]=i;
	}

为什这样建树可以建出正确的bst呢？

我们举个例子

比如3 2 4 1这个序列

排序后变为了1(4) 2(2) 3(1) 4(3)

括号内为权值，括号外为下标

第一步，插入1(4)

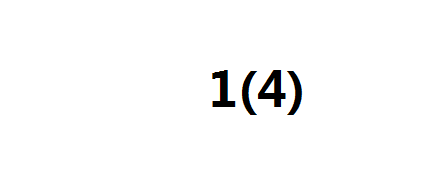
第二步，插入2(2)因为在单调队列中我们将其压掉了所以，将1(4)a插入到2(2)的左子树中

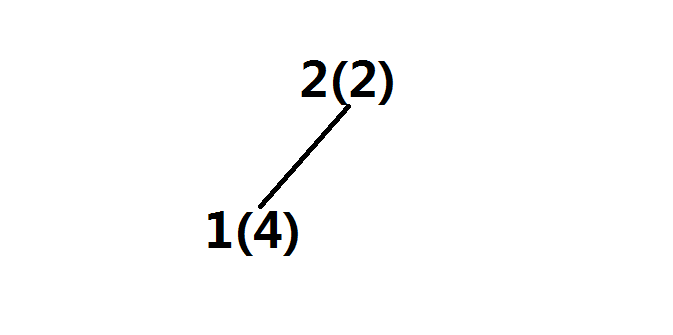
第三步

同理

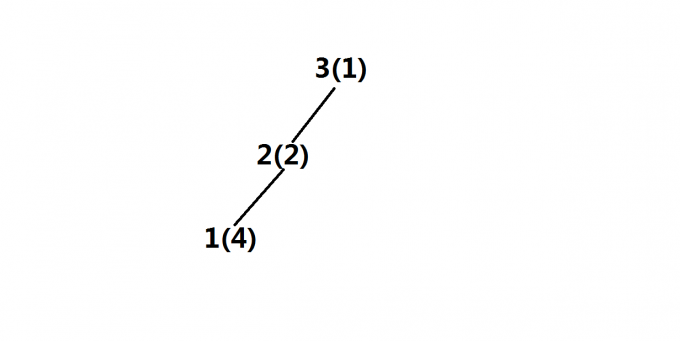
第四步，目前单调队列中只有3(1)新点4(3)进入后无法压掉3(1)便放在3(1)的左子树中

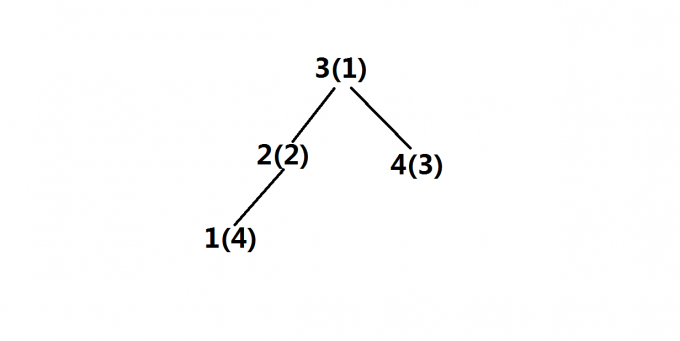
建树完毕，我们按权值加入，每进入一个点便插入到目前的合适位置，当更优的点

出现时，倘若恰好将此点压掉，我们便将上一个点与该点的连接关系断开，将新节

点插入到这两个节点之间，如下图

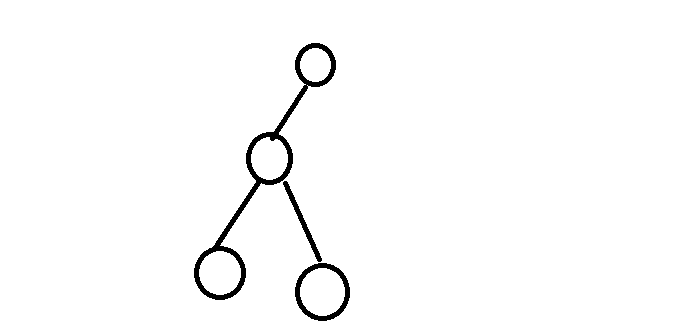
红色为新加入节点

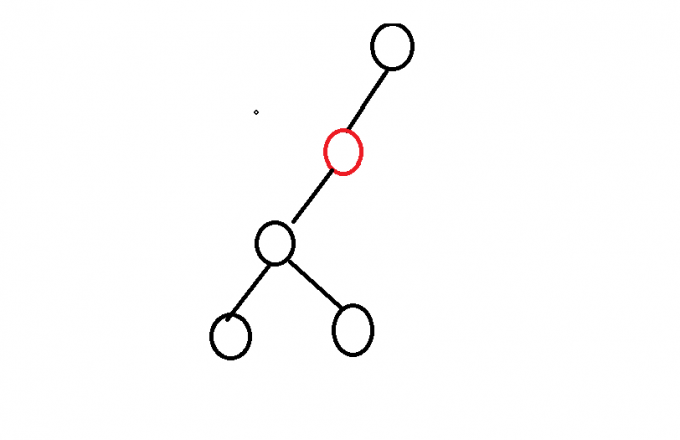
为什么后续加入的节点不会插到以经压入的节点下呢？得益于我们加入节点是按权值从小到大加入的

比如说上图，既然红色节点已经入队列了，能红色节点的子树中插入的节点一定小于红色节点的权值，但已经没有了

这就是整个算法的思路

完整代码如下

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int maxn=1e6+10;
inline int read(){
	int ret=0;
	int f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-'){
			f=-f;
		}
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		ret=ret*10+(ch^'0');
		ch=getchar();
	}
	return ret*f;
}
int q[maxn];
int l[maxn];
int r[maxn];
int a[maxn];
int n;
void dfs(int ro){
	if(!ro){
		return ;
	}
	cout<<ro<<" ";
	dfs(l[ro]);
	dfs(r[ro]);
	return ;
}
int main(){
	n=read();
	int x;
	for(int i=1;i<=n;i++){
		x=read();
		a[x]=i;
	}
	int tot=0;
	int pos=0;
	for(int i=1;i<=n;i++){
		tot=pos;
		while(pos&&a[q[pos]]>a[i]){
			pos--;
		}
		if(pos){
			r[q[pos]]=i;
		}
		if(pos<tot){
			l[i]=q[pos+1];
		}
		q[tot=++pos]=i;
	}
	dfs(q[1]);
	return 0;
}

完结撒花!