Codeforces 1340B Nastya and Scoreboard(dp，贪心)

题目链接OvO

题目大意

  给你\(n\)串数字，\(1\)代表该位置是亮的，\(0\)代表是灭的。你必须修改\(k\)个数字，使某些\(0\)变为\(1\)。注意，只能把原来的\(0\)改成\(1\)。

分析

  由于每串数字上的\(1\)是不能修改的，所以每串数字并不一定能完整的表示\(0-9\)之内的所有数，所有需要先对每串数字做一下预处理，计算出能改为哪些数字和修改的代价。然后第一步，我们需要判断是否可以构成\(n\)个完整数字。这个直接来判断似乎不太好做。但是可以转换一下，变成能否只消耗\(k\)构成\(n\)个完整数字。这个类似于背包问题，问能否用\(n\)个数构成\(k\)。

  状态转移方式为：若第\(i\)步可以到达容量\(j\)，那么第\(i+1\)步就可以到达\(j+cost[i+1]\)。

  我们将上面稍微变形，不难得出：\(dp[i][j] |= dp[i-1][j-cost[i][t]],0\leq t\leq 9\)。

  所以只要判断\(dp[n][k]\)是否为\(true\)就能知道能否只消耗\(k\)显示\(n\)个完整数字了。但是这还不够，答案还需要输出最大的可能结果。我们通过上面的\(dp\)已经获得了一个状态转移的图，红色终点代表错误的终点，黑色终点代表正确的终点画出来(只是部分)大概是这样子的(这里只有\(end1\)是正确的，其他的要么是容量不为\(k\)(\(end2\))，要么是选的个数不够(\(end3\)))：



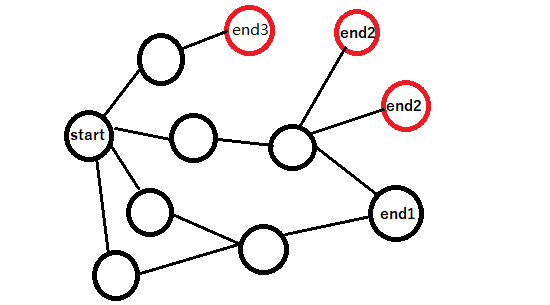
  我们的\(dp\)数组里存储了从起始点到终点的所有路径，可以看出，只要从终点向起点方向走，一定能走到起点，每次消耗为\(cost[i][t]\)。但是题目要求我们输出答案最大，答案最大的话就要要求大的数字靠前，所以倒着从最后一个数开始贪心肯定是不行的，我们需要正着贪心。那么我们就只能倒着\(dp\)，这样我们就得到一个从最后一个数到第一个数的状态转移图。这时候我们只需要从第一个数开始贪心的每步选择能够到达的，代表数字最大的路径就行了。这样的话第一步的状态转移方程就变成了\(dp[i][j] |= dp[i+1][j-cost[i][k]],0\leq t\leq 9\)。

具体实现

第一步

  先预处理，求每串数变成每个数字的消耗，显示不了的数字消耗就是\(-1\)，存入\(cost\)数组中。

    char nums[][10] = {"1110111","0010010","1011101","1011011","0111010","1101011","1101111","1010010","1111111","1111011"};
    char str[maxn][10];
    void solve(int pos) {
        for (int i = 9; i>=0; --i) {
            int cnt = 0;
            for (int j = 0; j<7; ++j) {
                if (str[pos][j]=='1'&&nums[i][j]=='0') {
                    cnt = -1;
                    break;
                }
                if (str[pos][j]=='0'&&nums[i][j]=='1') ++cnt;
            }
            cost[pos][i] = cnt;
        }
    }

第二步

  根据\(dp[i][j] |= dp[i+1][j-cost[i][k]],0\leq t\leq 9\)倒着得到\(dp\)数组的值。

        dp[n+1][0] = true;
        for (int i = n; i>=1; --i)
            for (int k = 9; k>=0; --k)
                if (~cost[i][k])
                    for (int j = m; j>=cost[i][k]; --j)
                        dp[i][j] |= dp[i+1][j-cost[i][k]];
        if (!dp[1][m]) {
            cout << -1 << endl;
            return 0;
        }

第三步

  正着贪心得到最大可能的数字。

        for (int i = 1; i<=n; ++i)
            for (int j = 9; j>=0; --j)
                if (~cost[i][j] && m>=cost[i][j] && dp[i+1][m-cost[i][j]]) {
                    cout << j;
                    m -= cost[i][j];
                    break;
                }

完整代码

    const int maxn = 2e3+10;
    char nums[][10] = {"1110111","0010010","1011101","1011011","0111010","1101011","1101111","1010010","1111111","1111011"};
    char str[maxn][10];
    int n, m, dp[maxn][maxn], cost[maxn][10];
    void solve(int pos) {
        for (int i = 9; i>=0; --i) {
            int cnt = 0;
            for (int j = 0; j<7; ++j) {
                if (str[pos][j]=='1'&&nums[i][j]=='0') {
                    cnt = -1;
                    break;
                }
                if (str[pos][j]=='0'&&nums[i][j]=='1') ++cnt;
            }
            cost[pos][i] = cnt;
        }
    }
    int main(void) {
        cin >> n >> m;
        for (int i = 1; i<=n; ++i) {
            cin >> str[i];
            solve(i);
        }
        dp[n+1][0] = true;
        for (int i = n; i>=1; --i)
            for (int k = 9; k>=0; --k)
                if (~cost[i][k])
                    for (int j = m; j>=cost[i][k]; --j)
                        dp[i][j] |= dp[i+1][j-cost[i][k]];
        if (!dp[1][m]) {
            cout << -1 << endl;
            return 0;
        }
        for (int i = 1; i<=n; ++i)
            for (int j = 9; j>=0; --j)
                if (~cost[i][j] && m>=cost[i][j] && dp[i+1][m-cost[i][j]]) {
                    cout << j;
                    m -= cost[i][j];
                    break;
                }
        cout << endl;
        return 0;
    }