MergeSort归并排序和利用归并排序计算出数组中的逆序对

　　首先先上LeetCode今天的每日一题（面试题51. 数组中的逆序对）：

　　在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

//输入: [7,5,6,4]
//输出: 5

示例1

　　由于题目中已经给出数组长度为： 0 <= 数组长度 <= 50000， 所以如果单纯使用两个for循环（时间复杂度为 $O\left ( n^{2} \right )$ 暴力求解的话是一定会超时的。

　　在这里可以使用归并排序，并同时得出逆序对的总数，其中归并排序使用的是“分治法”，所以时间复杂度为 $O\left ( nlogn \right )$ ，而计算逆序对只需要在每次循环中进行一次计算，所以相当于在其中增加 $O\left ( 1 \right )$ 的时间复杂度，所以时间复杂度并不会变化，这个在后面会对计算方法会有详细的介绍，因为一开始自己写的时候也有在这里卡住。

　　如下是归并排序的示意图，图是盗来的，但是觉得做的真的是太好看了，而且清楚明了，以下超链接为引用的原博客网址（https://www.cnblogs.com/chengxiao/p/6194356.html）：

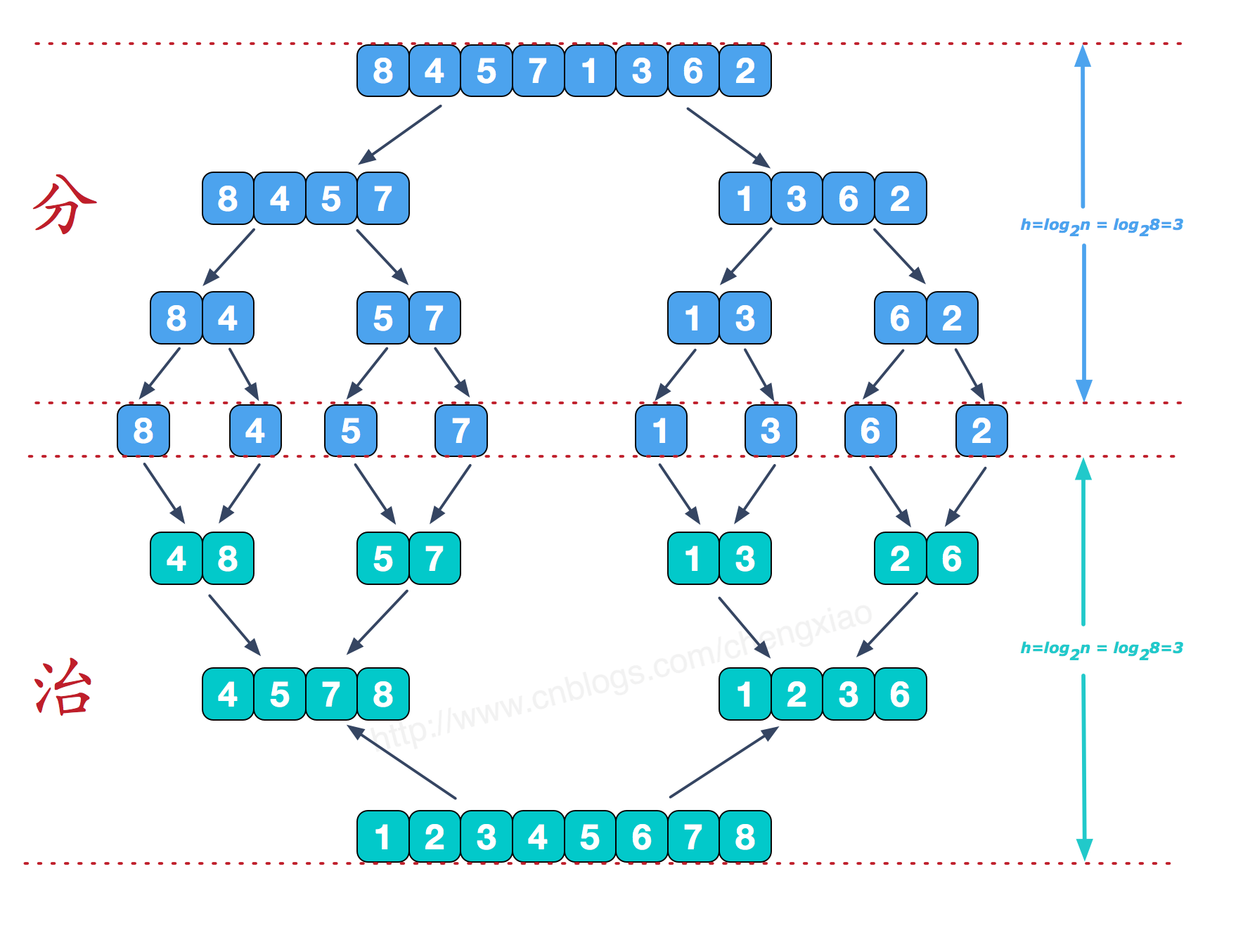
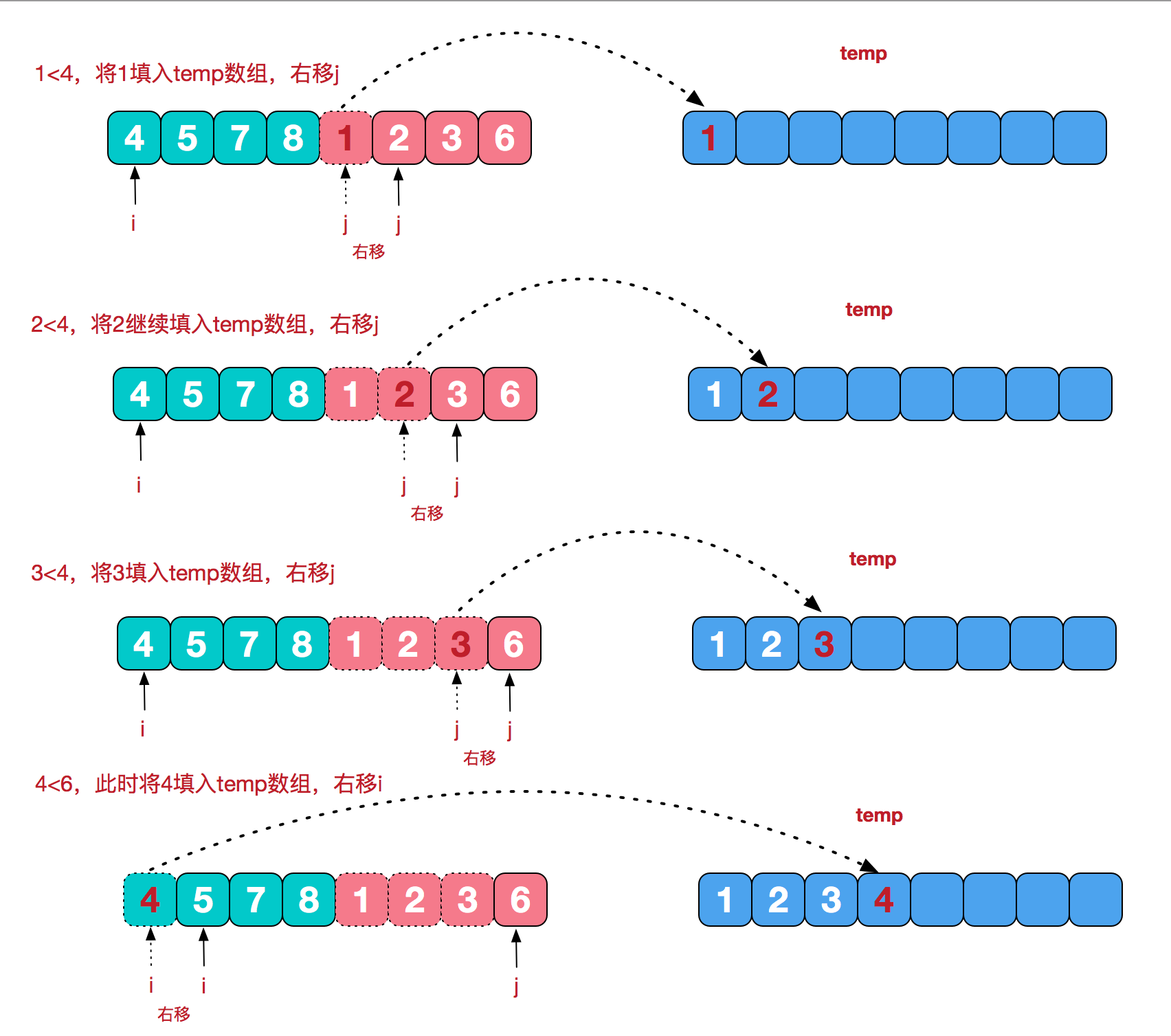
　　相信看了这张图之后，整个归并排序的算法就已经非常清楚明了了，如下代码是只对于归并排序的实现，使用的是递归的方法：

public class mergeSort {
    public static void main(String args[]) {
        mergeSort a = new mergeSort();
        int[] numbers = new int[] {7,2,5,2,6,3,4,8};
        a.merge(0, numbers.length-1, numbers);
        for (int i : numbers) {
            System.out.println(i);
        }
    }
    public void merge(int left, int right, int[] numbers) {
        if(left < right) {
            int mid = (left + right)/2;
            merge(left, mid, numbers);
            merge(mid+1, right, numbers);;
            mergeSort(left, right, numbers);
        }
    }
    public void mergeSort(int left, int right, int[] numbers) {
        //将数组分为左右两个部分，分别为[left, mid]和[mid+1, right]
        int mid = (left + right)/2;
        int i = left;
        int j = mid + 1;
        int[] temp = new int[right - left + 1];
        for(int k = 0 ; k < temp.length; k++) {
            //考虑如果数组左边已经到达尾端，则只需要将右边数组依次放入temp数组即可
            if(i == mid + 1) {
                temp[k] = numbers[j];
                j++;
            }
            //考虑如果数组右边已经到达尾端，则只需要将左边数组依次放入temp数组即可
            else if(j == right + 1) {
                temp[k] = numbers[i];
                i++;
            }
            //如果左边数组指向的数字大于右边数组指向的数字，则将右边数组指向的数字放入temp数组当中
            else if(numbers[i] > numbers[j]) {
                temp[k] = numbers[j];
                j++;
            }
            //反之亦然
            else {
                temp[k] = numbers[i];
                i++;
            }
        }
        //最后将排好序的temp数组重新放入原数组当中，记得起始位置是从numbers数组的left开始，而不是0
        for(int m = left, k = 0; m <= right; m++, k++) {
            numbers[m] = temp[k];
        }
    }
}

//最终结果为：2,2,3,4,5,6,7,8

归并排序的实现

　　那么，如何来计算出逆序对呢？那么我们就要思考，为什么在归并排序中就能计算出逆序对的数量。这就要观察每次用来排序的数组的特点了，由于排序是由从两个长度为1的数组开始进行的，所以就可以保证在每一次的递归过程中，我们需要进行排序的数组一定会有以下规律，即：

　　1. 将要排序的数组number的左右两个部分一定都是已经分别排好序了的，例如上图中需要排序的数组[4，5，7，8，1，2，3，6]， 将这个数组分为左右两个部分[4，5，7，8]和[1，2，3，6]，这两个数组是一定已经排好顺序了的。

　　2. 每个数字与其他数组都会正好比一次大小，例如上图中的数字4，它在这次的统计中，会跟1，2，3，6比，会发现有3组逆序对，而在那之后，这个4就再也不会跟这4给数字进行比较了，也就不会产生重复。

　　这时，你一定会问，那前面的5，7，8又是在什么时候进行比较的呢？其实在上一步，即当大的数组为[4，5，7，8]的时候，4就已经和7,8进行了比较，而在更前一步，4就和5进行了比较，所以就可以完美的不重复不遗漏统计所有数字的逆序对了。

　　既然不会重复，那我们也就只需要有一个计数器count来记录产生的逆序对的数量就行了，那么，怎么来计算这个逆序对的数量呢？

　　我一开始的错误想法是，左边数组的每一个数字和右边数字进行比较的时候，如果发现左边数字大于右边，那么count就＋1，但发现统计的数量总是少于实际值，后来才发现了原因：

　　例如数组[2，2，4，5，3，，6，8]， 将其看为左右两个部分，可以发现当左边数组指针指向5的时候，右边数组的指针已经指向4了，那么其实本来数组中的5和3是并没有进行比较的，因此就会出现漏数的情况。

　　在观察了很久之后，终于发现了其中的规律：

　　假设左边数组指针为 $i$ ， 右边数组指针为 $j$ ， 如果发现 $ numbers[i] > numbers[j]$ ， 那么对于右边数组的这个数字 $numbers[j]$ ，一定有左边数组的 $[i, mid]$ 位置的数字都会大于这个数字,因为这里两边的数组都是递增的，所以我们只需要每次发现 $numbers[i] > numbers[j]$ 之后，用 $count = count + (mid - i + 1)$ 统计即可。

　　注意：为了统计count的数量，一定要将方法中的返回值类型从 void 变为 int， 因为如果只是利用void方法传参的话，count的值是不会改变的。（如有错误，欢迎指正，应该是这个样子的吧）

　　最终利用归并排序计算逆序对的代码实现如下：

public class Merge_Sort {
    public static void main(String args[]) {
        Merge_Sort a = new Merge_Sort();
        int[] numbers = new int[] {4,2,5,2,6,3,4,8};
        int b = a.merge(0, numbers.length-1, numbers);
        System.out.println(b);
    }
    public int merge(int left, int right, int[] numbers) {
        if(left < right) {
            int mid = (left + right)/2;
            int count = merge(left, mid, numbers) + merge(mid+1, right, numbers);;
            return mergeSort(left, right, numbers, count);
        }
        return 0;

    }
    public int mergeSort(int left, int right, int[] numbers, int count) {
        int mid = (left + right)/2;
        int i = left;
        int j = mid + 1;
        int[] temp = new int[right - left + 1];
        for(int k = 0 ; k < temp.length; k++) {
            if(i == mid + 1) {
                temp[k] = numbers[j];
                j++;
            }
            else if(j == right + 1) {
                temp[k] = numbers[i];
                i++;
            }
            else if(numbers[i] > numbers[j]) {
                temp[k] = numbers[j];
                j++;
                //count计数代码添加如下
                count = count + (mid - i + 1);
            }
            else {
                temp[k] = numbers[i];
                i++;
            }

        }
        for(int m = left, k = 0; m <= right; m++, k++) {
            numbers[m] = temp[k];
        }
        return count;
    }
}
//输出结果为8