PHP实现堆排序

经验

工作了，面试我工作这家公司时被技术面打击得不行，因为自己的数据结构等基础学得实在太差，虽然原来是想做设计师的说。。。不过看在PHP写得还凑合的份上能来实习了，但还是决心恶补一下基础。 其实自己之前也确实感觉到了基础的重要性，一些比较深的东西都比较底层，不学好根本没法进行。像我之前用PHP做websocket，就牵扯到数据包、数据帧等概念，搞不清楚，连数据都没法处理，还得后来补。所以我准备重新学一下数据结构,算法,网络等基础知识，也在此跟大家提个醒,别像我一样走反了方向，甚至到明白过来就已经晚了。

今天来说一下被问到的堆排序的问题，当时被问到时，连完全二叉树的概念都忘了。不过幸好我还有一点点数据结构基础，看了点资料也有些明白了，所以想用PHP写一下二叉树的堆排序，顺便也复习下二叉树，堆等数据结构。

---

堆

堆(heap)是计算机科学中一类特殊的数据结构的统称，通常是一个可以被看做一棵树的数组对象。

堆{k1,k2,ki,…,kn} (ki <= k2i,ki <= k2i+1)|(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4...n/2)

关于堆：

• 堆中某个节点的值总是不大于或不小于其父节点的值；
• 堆总是一棵完全二叉树（下面）。
• 将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

---

完全二叉树

说到堆排序，就不能不提完全二叉树，这些基本概念在网上到处都是，我摘了个最简单的。。

完全二叉树：除最后一层外，每一层上的节点数均达到最大值；在最后一层上只缺少右边的若干结点。

我自己总结认为，正是因为有下面两个特点，

• 只允许最后一层有空缺结点且空缺在右边，即叶子结点只能在层次最大的两层上出现（存储方式的规则性）；
• 若i>1，tree的双亲为tree[i div 2]（其父子结点值的规律性）；

才使得其进行排序非常方便。

---

堆排序

堆排序求升序用大顶堆，求降序用小顶堆。

本例用求降序的小顶堆来解析。

堆排序步骤如下：

1、我们将数据（49、38、65、97、76、13、27、50）建立一个数组$arr；

2、用数组$arr建立一个小顶堆（主要步骤，会在代码注释里解释，下图是用一个数组建立小顶堆的过程）；

3、将堆的根（最小的元素）与最后一个叶子交换，并将堆长度减一，跳到第二步；

4、重复2-3步，直到堆中只有一个结点，排序完成。

---

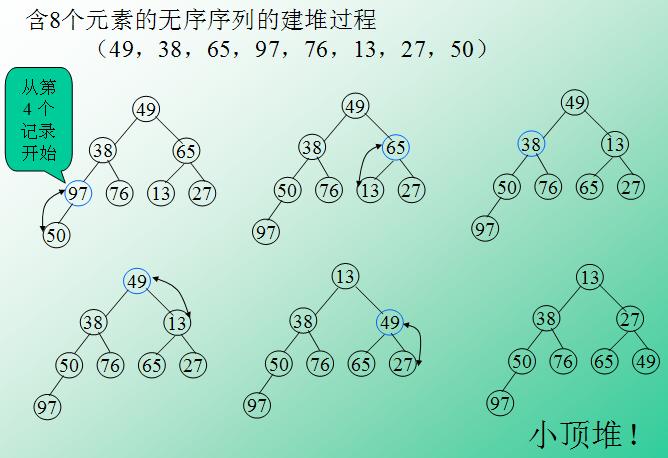
堆排序的PHP实现

//因为是数组,下标从0开始,所以,下标为n根结点的左子结点为2n+1,右子结点为2n+2;
//初始化值,建立初始堆
$arr=array(49,38,65,97,76,13,27,50);
$arrSize=count($arr);

//将第一次排序抽出来，因为最后一次排序不需要再交换值了。
buildHeap($arr,$arrSize);

for($i=$arrSize-1;$i>0;$i--){
    swap($arr,$i,0);
    $arrSize--;
    buildHeap($arr,$arrSize);
}

//用数组建立最小堆
function buildHeap(&$arr,$arrSize){
    //计算出最开始的下标$index,如图,为数字"97"所在位置,比较每一个子树的父结点和子结点,将最小值存入父结点中
    //从$index处对一个树进行循环比较,形成最小堆
    for($index=intval($arrSize/2)-1; $index>=0; $index--){
        //如果有左节点,将其下标存进最小值$min
        if($index*2+1<$arrSize){
            $min=$index*2+1;
            //如果有右子结点,比较左右结点的大小,如果右子结点更小,将其结点的下标记录进最小值$min
            if($index*2+2<$arrSize){
                if($arr[$index*2+2]<$arr[$min]){
                    $min=$index*2+2;
                }
            }
            //将子结点中较小的和父结点比较,若子结点较小,与父结点交换位置,同时更新较小
            if($arr[$min]<$arr[$index]){
                swap($arr,$min,$index);
            }
        }
    }
}

//此函数用来交换下数组$arr中下标为$one和$another的数据
function swap(&$arr,$one,$another){
    $tmp=$arr[$one];
    $arr[$one]=$arr[$another];
    $arr[$another]=$tmp;
}

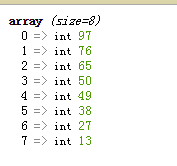
下面是排序的最终结果：

---

2017.12.07 添加：

堆用来进行全排序，时间复杂度是 O(nlogn)

而快排用来全排序，平均时间复杂度也是 O(nlogn)

但堆排序可以用来求 TopK 时，堆的时间复杂度为 O(Klog2(n)，因为它只需要进行 K 轮排序即可。

如果您觉得本博文对您有帮助，您可以推荐或关注我，如果您有什么问题，可以在下方留言讨论，谢谢。

h2:first-child, body>h1:first-child, body>h1:first-child+h2, body>h3:first-child, body>h4:first-child, body>h5:first-child, body>h6:first-child {
margin-top: 0;
padding-top: 0;
}

a:first-child h1, a:first-child h2, a:first-child h3, a:first-child h4, a:first-child h5, a:first-child h6 {
margin-top: 0;
padding-top: 0;
}

h1+p, h2+p, h3+p, h4+p, h5+p, h6+p {
margin-top: 10px;
}

/* LINKS
=============================================================================*/

a {
color: #4183C4;
text-decoration: none;
}

a:hover {
text-decoration: underline;
}

/* LISTS
=============================================================================*/

ul, ol {
padding-left: 30px;
}

ul li > :first-child,
ol li > :first-child,
ul li ul:first-of-type,
ol li ol:first-of-type,
ul li ol:first-of-type,
ol li ul:first-of-type {
margin-top: 0px;
}

ul ul, ul ol, ol ol, ol ul {
margin-bottom: 0;
}

dl {
padding: 0;
}

dl dt {
font-size: 14px;
font-weight: bold;
font-style: italic;
padding: 0;
margin: 15px 0 5px;
}

dl dt:first-child {
padding: 0;
}

dl dt>:first-child {
margin-top: 0px;
}

dl dt>:last-child {
margin-bottom: 0px;
}

dl dd {
margin: 0 0 15px;
padding: 0 15px;
}

dl dd>:first-child {
margin-top: 0px;
}

dl dd>:last-child {
margin-bottom: 0px;
}

/* CODE
=============================================================================*/

pre, code, tt {
font-size: 12px;
font-family: Consolas, "Liberation Mono", Courier, monospace;
}

code, tt {
margin: 0 0px;
padding: 0px 0px;
white-space: nowrap;
border: 1px solid #eaeaea;
background-color: #f8f8f8;
border-radius: 3px;
}

pre>code {
margin: 0;
padding: 0;
white-space: pre;
border: none;
background: transparent;
}

pre {
background-color: #f8f8f8;
border: 1px solid #ccc;
font-size: 13px;
line-height: 19px;
overflow: auto;
padding: 6px 10px;
border-radius: 3px;
}

pre code, pre tt {
background-color: transparent;
border: none;
}

kbd {
-moz-border-bottom-colors: none;
-moz-border-left-colors: none;
-moz-border-right-colors: none;
-moz-border-top-colors: none;
background-color: #DDDDDD;
background-image: linear-gradient(#F1F1F1, #DDDDDD);
background-repeat: repeat-x;
border-color: #DDDDDD #CCCCCC #CCCCCC #DDDDDD;
border-image: none;
border-radius: 2px 2px 2px 2px;
border-style: solid;
border-width: 1px;
font-family: "Helvetica Neue",Helvetica,Arial,sans-serif;
line-height: 10px;
padding: 1px 4px;
}

/* QUOTES
=============================================================================*/

blockquote {
border-left: 4px solid #DDD;
padding: 0 15px;
color: #777;
}

blockquote>:first-child {
margin-top: 0px;
}

blockquote>:last-child {
margin-bottom: 0px;
}

/* HORIZONTAL RULES
=============================================================================*/

hr {
clear: both;
margin: 15px 0;
height: 0px;
overflow: hidden;
border: none;
background: transparent;
border-bottom: 4px solid #ddd;
padding: 0;
}

/* TABLES
=============================================================================*/

table th {
font-weight: bold;
}

table th, table td {
border: 1px solid #ccc;
padding: 6px 13px;
}

table tr {
border-top: 1px solid #ccc;
background-color: #fff;
}

table tr:nth-child(2n) {
background-color: #f8f8f8;
}

/* IMAGES
=============================================================================*/

img {
max-width: 100%
}
-->