Treap 实现名次树

在主流STL版本中，set，map，都是BST实现的，具体来说是一种称为红黑树的动态平衡BST；

但是在竞赛中并不常用，因为红黑树过于复杂，他的插入 5 种，删除 6 中，代码量极大（如果你要改板子的话）；

相比之下有一种Treap的动态平衡BST，却也可以做到插入，删除，查找的期望时间复杂度O(logn)；

结点定义：

struct Node {
    Node *ch[];
    int r;  //优先级
    int v;  //值
    int s;  //结点总数

    Node(int v):v(v) {
        ch[] = ch[] = NULL;
        r = rand();
        s = ;
    }

    bool operator < (const Node& rhs) const {
        return r < rhs.r;
    }

    int cmp(int x) const {
        if(x==v) return -;
        return x < v ? :;
    }

    void maintain() {
        s = ;
        if(ch[]!=NULL) s +=ch[]->s;
        if(ch[]!=NULL) s +=ch[]->s;
    }
};

我这里加了一些看似不需要的东西s，而这个 s却是Treap相比BST的闪光点！！！

动态平衡二叉树 BST 的性质 v，值，根大于左子树，小于右子树； cmp函数，插入，删除时，小于 v，返回 0；

r   : 堆的性质，大根堆，根优先级最高；

旋转操作是一个坎，虽然不难，但是好多书籍上面感觉欲言又止；

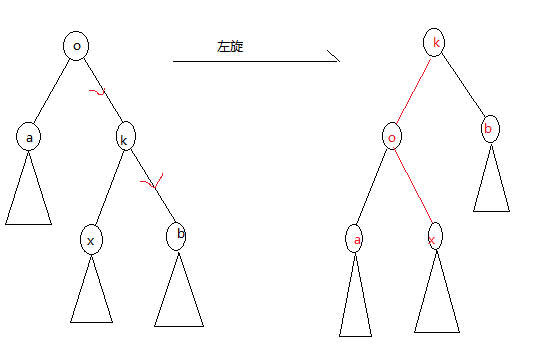
左旋： 由于 堆的性质，可能使得 BST 不对（插入，删除），需要旋转，比如说，o点的优先级小于 k 点的优先级，要左旋，（大于，相反）

这个时候要是还想满足BST的性质，只需要改动几个点，就ok了。

//旋转
void rotate(Node* &o,int d) {
    Node* k = o->ch[d^];
    o->ch[d^] = k->ch[d];
    k->ch[d] = o;
    o->maintain();
    k->maintain();
    o = k;
}

同时，maintain函数，要重新统计节点数。

插入操作；

首先按照普通的BST递归插入；

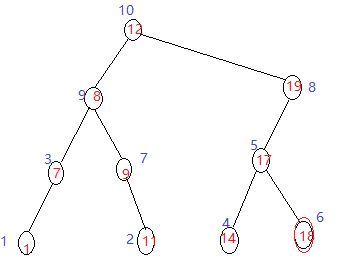
插入后，发现，此时的堆性质已经不满足了；要进行递归旋转！！！

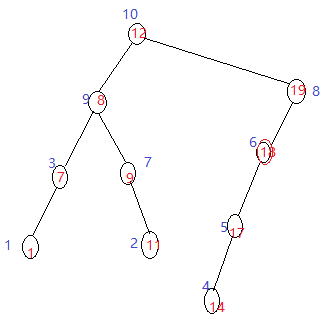
//插入
void insert(Node* &o,int x) {
    if(o==NULL) o = new Node(x);
    else {
        int d = (x< o->v?:);  //可能有相同的元素要插入
        insert(o->ch[d],x);
        if(o->ch[d]->r > o->r)
            rotate(o,d^);
    }
    o->maintain();
}

同样，每次递归到一层，重新维护节点信息；

删除操作：

首先递归找到这个结点；

这个结点如果左子树为空，或者右子树为空，很好解决；相反的子树代替父节点；

要是两者都有怎么解决？保持堆的性质 和 BST的性质？

先不急于删去点，首先比较一下左右子树的优先级，把优先级较高的子树旋转到根；

例如上图中，加入 k 较高，右旋到左边的图；然后递归删除 k ，这样就保证了整个Treap树的性质！！！

//删除
void remove(Node* &o,int x) {
    int d = o->cmp(x);
    if(d==-) {
        Node* u = o;
        if(o->ch[]!=NULL&&o->ch[]!=NULL) {
            int d2 = (o->ch[]->r > o->ch[]->r ?  : );
            rotate(o,d2);
            remove(o->ch[d2],x);
        }
        else {
            if(o->ch[]==NULL)
                o = o ->ch[];
            else o = o ->ch[];
        }
    }
    else {
        remove(o->ch[d],x);
    }
    if(o!=NULL) o->maintain();
}

注意：插入，删除，的时候没有去检查，可以先去检查了一下，这样就完全和set是一样的了

int find(Node* o,int x) {
    while(o!=NULL) {
        int d = o->cmp(x);
        if(d==-) return ; //存在
        else o = o->ch[d];
    }
    return ;   //不存在
}

到了这里就已经完全实现了Treap树了，很happy\(^o^)/~

但是：

如果说，Treap树和 set 是一样的，那就没必要写 Treap了，举个栗子！

名次树！！！

个人柑橘往左子树走很巧妙， (＾－＾)V

利用右子树有多少节点而往左子树走；

//名次树
Node* root[maxn];

//第 k 大的值
int kth(Node* o,int k) {
    if(o==NULL||k<=||k>o->s) return ;
    int s = (o->ch[]==NULL ? : o->ch[]->s);
    if(k==s+) return o->v;
    else if(k<=s) return kth(o->ch[],k);
    else return kth(o->ch[],k-s-);
}