Splay浅谈

Splay是众多平衡树之一，它的功能十分强大，但常数极大。在LCT和许多数据结构中都能用到。

Splay的核心操作，就是rotate。为了使树不是一条链，而是平衡的，我们需要旋转来维护形态。理论很简单，下面来看一下如何实现。

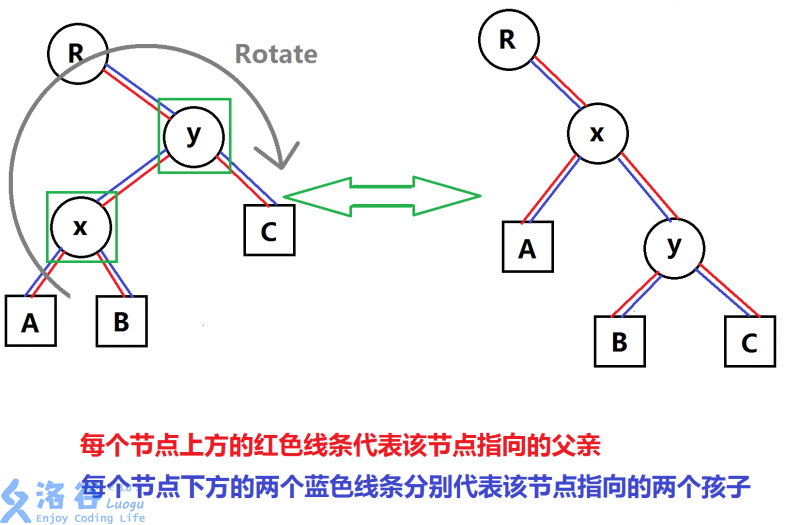
图片转自洛谷

我们注意到，旋转之后，这棵树依然保持着正常的大小关系。

来尝试着写代码。

观察到，y的c儿子依旧是y的右儿子，而x，y的父子关系发生了改变，x的左儿子不变，x的右儿子变成了y的左儿子。

这是右旋。

明显的，我们发现不只有这一种情况。单旋的Splay，会被出题人的构造数据卡成链。我们先来处理双旋操作，再来处理链。

Rotate：

inline void rotate(node *x){
    node *y=x->fa,*z=y->fa;int k=y->ch[1]==x;
    z->ch[z->ch[1]==y]=x;x->fa=z;
    y->ch[k]=x->ch[k^1];x->ch[k^1]->fa=y;
    x->ch[k^1]=y;y->fa=x;pushup(y);pushup(x);
}

注意，结构体里面存了x节点的父亲，左右儿子，值，子树大小以及此处值相同的节点个数。

其中，k=1表示y的右儿子是x，这是逻辑表达式。

理解了rotatw操作，开始讲一下它的核心：Splay操作。

还记得我说的单旋吗？在一些情况下，如果你只旋转当前节点，会依旧成为一条链。

我们如何避免这件事呢？

我们观察到，当x，x的fa以及grandfa在一条线上时，转x是无意义的。

所以，我们要rotate(y).

就这么简单。

这样一直到x转到目标点。

代码：

inline void splay(node *x,node *goal){
    node *y,*z;
    while(x->fa!=goal){
        y=x->fa,z=y->fa;
        if(z!=goal)(z->ch[1]==y)^(y->ch[1]==x)?rotate(x):rotate(y);
        rotate(x);
    }if(goal==null)rt=x;
}

注意，此处我用的是指针，所以不是!goal，而是goal==null.

下面，就Splay模板开始讲解。

首先，插入操作。

我们插入一个点，首先判断，如果它是一棵空树，那就把树的根节点新建出来(指针)，值为插入的值，return即可。

否则，往下沉。

有两种可能：在树中找的过程中，如果有值一样的，就把x旋转到根，并且把x的num++.

否则，新建节点，记录最后找到的点。

最后找到的点是新建点的father.

插入的值是新建点的值。

插入完成。

代码有些冗长，注意理解背诵。

inline node *new_(){
    node *x=new node;
    x->ch[0]=x->ch[1]=x->fa=null;x->siz=x->num=1;return x;
}
inline void insert(int v){
    node *x=rt;
    if(x==null){rt=new_();rt->v=v;return;}
    node *fa=null;
    while(x!=null){
        fa=x;if(v!=x->v)x=x->ch[v>=x->v];
        else {splay(x,null);x->siz++;x->num++;return;}
    }x=new_();fa->ch[v>=fa->v]=x;
    x->fa=fa;x->v=v;
    splay(x,null);
}

下一步操作，删除（del，Del）

首先，我们知道，删除的值一定在树中。

于是，我们从根开始搜索。

找到之后，对于这个点，进行del.

先把这个点(x)splay到根，并且把它的子树大小(siz)和同值节点数量(num)--.

这时，有两种结果。

首先，于这个点相同值的点还有。

这样，直接return即可。

否则，如果这棵树只有这一个点，那就把根赋值为null，然后return即可。

否则，顺着x的左右孩子向下找。

找到最后的节点，把它旋转到x的孩子上。

这需要更新x了，也就是删除。

x的孩子认y(转上来的节点)做爹，y是根，爹为null，delete(x)即可。

删除完成。

代码：

inline void del(node *x){
    splay(x,null);x->siz--;x->num--;int k;
    if(x->num)return;
    if(x->ch[0]!=null)k=0;
    else if(x->ch[1]!=null)k=1;
    else {rt=null;delete(x);return;}
    node *y=x->ch[k];
    while(y->ch[k^1]!=null)y=y->ch[k^1];
    splay(y,x);y->ch[k^1]=x->ch[k^1];
    x->ch[k^1]->fa=y;y->fa=null;rt=y;
    delete(x);
}inline void Del(int v){
    node *x=rt;
    while(x!=null){
        if(v!=x->v)x=x->ch[v>=x->v];
        else {del(x);return;}
    }
}

然后，就是最熟悉的求排名，求排名为k的数，以及前驱，后继。

rank：首先找v是否存在。不存在输出0.

如果存在，那么它的排名就是当前点的左孩子的子树大小+1.

完成。

求排名为k的数：

定义c为当前点的左子树大小。

如果当前点的左子树大小超过了k，说明它不是要找的点，向它的左子树找。

如果c<k了，说明找到了。

k就把c和当前点的num减掉。

如果k<0了，输出当前x的值即可。

否则，找x的右子树。

完成。

一起说前驱后继吧。

前驱，小于v的最大数。

后继，大于v的最小数。

从根开始搜索，定义一个极值用来更新。

这个不好阐述，看代码理解吧。

上代码：

inline int rank(int v){
    node *x=rt;
    while(x!=null){
        if(v>x->v)x=x->ch[1];
        else if(v<x->v)x=x->ch[0];
        else{splay(x,null);return x->ch[0]->siz+1;}
    }return 0;
}inline int kth(int k){
    node *x=rt;int c;
    while(x!=null){
        c=x->ch[0]->siz;
        if(c>=k)x=x->ch[0];
        else{
            k-=c+x->num;
            if(k<=0){splay(x,null);return x->v;}
            x=x->ch[1];
        }
    }return 0;
}
inline int pre(int v){
    node *x=rt;int ans=-inf;
    while(x!=null){
        if(v>x->v)ans=max(ans,x->v),x=x->ch[1];
        else x=x->ch[0];
    }return ans;
}
inline int last(int v){
    node *x=rt;int ans=inf;
    while(x!=null){
        if(v<x->v)ans=min(ans,x->v),x=x->ch[0];
        else x=x->ch[1];
    }return ans;
}

至此，Splay告一段落。

Splay被称为序列之王，它还可以实现许多功能。

下次讲树套树的时候，一并说一下。

注：模板来自dalao——wjr.