blocks 单调栈、单调队列题解

blocks题解:

1、题面：

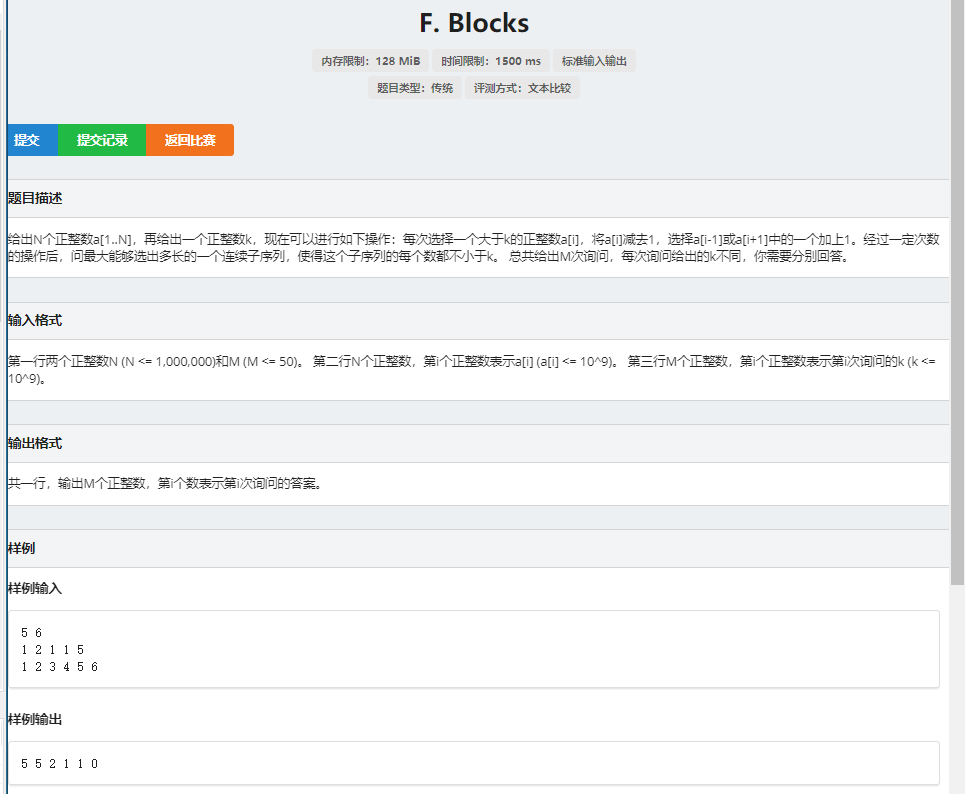
2、分析：

题意大概就是说，找一段最长的区间，并且这段区间的平均值>=k,那么我们可以对他的每一个值减去k，最终求和>=0即可。

那我们需要对每个可能的左端点和右端点进行考虑，并以此让他们进行配对，看他们之间的区间和是否非负。

那么我们先定住一个右端点，再依次考虑可能的左端点即可，那么左端点一开始会很自然的想到是所有小于k的点的右一个点，但是这样可能会T，那么在让我们优化一下，依照从左向右顺序找出所有可能合法的区间，并将出了他的左端点以外的所有点排除（因为这些点还可以向左拓展）但是这太麻烦了，所以我们可以从左向右（以上一个不合法区间的右端点的下一个点作为下一个不合法区间的左端点）找出不合法的区间，那么除了左右端点以外的任一点到左端点这一段区间一定是合法的，因为它没有被纳入进来，然后就找出了所有可能的左端点。那么就往一个单调递减栈里面堆数，注意一开始要在栈里push 0 。

3、代码：

不开long long 见祖宗

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ps push_back
#define mk make_pair
#define fi first
#define se second
typedef pair<ll,ll> pii;
const ll N=1e6+10;
ll n,m,sum[N],k,a[N];
stack<ll> q;
void clear(){
	while(q.size())
		q.pop();
}
int main(){
	cin>>n>>m;
//	ll x;
	for(ll i=1;i<=n;i++){
		scanf("%lld",&a[i]);
	}
	while(m--){
		cin>>k;
		clear();
		q.push(0);
		ll man=0;
		for(ll i=1;i<=n;i++)sum[i]=sum[i-1]+a[i]-k;
		for(ll i=1;i<=n;i++)if(q.empty()||sum[i]<sum[q.top()])q.push(i);
		for(ll i=n;i>=0;i--){
			ll jj=-1;
			while(!q.empty()&&sum[q.top()]<=sum[i]){
				jj=q.top();
				q.pop();
			}
			if(jj!=-1)man=max(man,i-jj);
		}
		cout<<man<<' ';
	}

}