冲刺 NOIP2024 之动态规划专题

• 专题链接

B - Birds

• \(3.19\) 。

混合背包 \(DP\) 。

定义 \(f_{i,j}\) 表示取到鸟巢 \(i\) ，获得 \(j\) 只小鸟时所剩的魔力值。

显然有 \(f_{0,0}=1\) 。

转移为：

\[f_{i+1,j+k}=\max(f_{i+1,j+k},\min(f_{i,j}-k\times cost_i+x,w+(j+k)\times b))
\]

其中 \(k\) 表示对于鸟巢 \(i\) 取了几个鸟，其余变量意义与上述表达或题面相同。

特别的，有任意 \(f_{i+1,j+k}\leq w+(j+k)\times b\) ，又题意可得。

注意：

• 将所有 \(f_{i,j}\) 初始化为 \(-1\) （表示没有更新过，而 \(0\) 可能是恰好为 \(0\) 并非未更新，会产生歧义），若 \(f_{i,j}\) 没有更新过，即他此时所剩魔力值 \(<0\) ，则无法更新 \(f_{i+1,j+k}\) 。

• 若 \(f_{i,j}-k\times cost_i<0\) 说明无法取这么多鸟，那么显然更大的 \(k\) 也无法取到，所以 \(break\) 。

• 对于 \(j\) 应循环到 \(sum_i\) ，\(sum_i\) 表示 \(c_i\) 的前缀和，即最多取这么多鸟。

  同理的，\(k\) 循环到 \(c_i\) 。

  当然，\(j,k\) 均从 \(0\) 开始循环。

最后处理答案，显然我们取完鸟巢 \(n\) 后的答案将体现在 \(f_{n+1,j}\) 中，答案为所有 \(\geq 0\) 的 \(f_{n+1,j}\) 中 \(j\) 的最大值。

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=1e3+10,M=1e4+10;
template<typename Tp> inline void read(Tp&x)
{
    x=0;register bool z=true;
    register char c=getchar();
    for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
    for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
    x=(z?x:~x+1);
}
int n,w,b,x,ans,c[N],v[N],sum[N],f[N][M];
signed main()
{
	#ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif
    read(n),read(w),read(b),read(x);
    for(int i=1;i<=n;i++)
        read(c[i]),
        sum[i]=sum[i-1]+c[i];
    for(int i=1;i<=n;i++) read(v[i]);
    memset(f,-1,sizeof(f));
    f[0][0]=w;
    for(int i=0;i<=n;i++)
        for(int j=0;j<=sum[i];j++)
            for(int k=0;k<=c[i];k++)
            {
                int s=f[i][j];
                if(s<0) break;
                s-=k*v[i];
                if(s<0) break;
                s=min(s+x,w+(j+k)*b);
                f[i+1][j+k]=max(f[i+1][j+k],s);
            }
    for(int i=0;i<=sum[n];i++)
        if(f[n+1][i]>=0)
            ans=max(ans,i);
    cout<<ans;
}

I - Game on Sum (Easy Version)

• \(3.20\) 。

此题为简单版，可以直接跑 \(DP\) 。

定义 \(f_{i,j}\) 表示进行了 \(i\) 轮，其中 \(Bob\) 选择加的有 \(j\) 轮时的分数。

设 \(x_i\) 表示 \(Alice\) 本轮选择的数。

• 若选择加，则有本轮分数为 \(f_{i-1,j-1}+x_i\) 。

• 若选择减，则有本轮分数为 \(f_{i-1,j}-x_i\) 。

显然 \(Bob\) 会选择 \(\min(f_{i-1,j-1}+x_i,f_{i-1,j}-x_i)\) 。

已知两者相加为定值，那么显然当两者相等时，\(\min(f_{i-1,j-1}+x_i,f_{i-1,j}-x_i)\) 最大。

所以 \(Alice\) 会选择两者相等时的情况，则有：

\[f_{i,j}=\min(f_{i-1,j-1}+x_i,f_{i-1,j}-x_i)=\dfrac{f_{i-1,j-1}+f_{i-1,j}}{2}
\]

同时，显然有 \(f_{i,0}=0\) ，\(f_{i,i}=i\times k\) 。

最后答案为 \(f_{n,m}\) 。

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=2010,P=1e9+7;
template<typename Tp> inline void read(Tp&x)
{
    x=0;register bool z=true;
    register char c=getchar();
    for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
    for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
    x=(z?x:~x+1);
}
int t,n,m,k,f[N][N],inv2;
int qpow(int a,int b)
{
    int ans=1;
    for(;b;b>>=1)
    {
        if(b&1) (ans*=a)%=P;
        (a*=a)%=P;
    }
    return ans;
}
signed main()
{
	#ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif
    read(t);
    inv2=qpow(2,P-2);
    while(t--)
    {
        read(n),read(m),read(k);
        for(int i=1;i<=n;i++)
            for(int j=0;j<=min(i,m);j++)
                if(i==j) f[i][j]=(k*i)%P;
                else if(j==0) f[i][j]=0;
                else f[i][j]=(((f[i-1][j]+f[i-1][j-1])%P)*inv2)%P;
        cout<<f[n][m]<<endl;
    }
}

Game on Sum (Hard Version)

• \(3.20\) 。

此题为困难版，将 \(n,m,t\) 的范围都大大增加，无法跑正常的 \(DP\) 。

所以去思考上面所述 \(DP\) 中关于答案的贡献。

不难发现，上述 \(DP\) 可以组成一个类似于杨辉三角的东西。

去考虑 \(f_{i,i}\) 对于答案的贡献，因为只有 \(f_{i,i}\) 在跑 \(DP\) 之前是确定的。

我们发现对于 \(f_{i,j}\) ，他将对 \(f_{i+1,j}\) 与 \(f_{i+1.j+1}\) 产生 \(1\) 的贡献（ \(1\) 指 $1\times $ 自身）。

那么以此类推，\(f_{i,i}\) 将对 \(f_{n,m}\) 产生 \(n-i\) 的贡献，其中选择 \(m-i\) 去加。

但同时如果从 \(f_{i,i}\) 去考虑的话，他还会给 \(f_{i+1,i+1}\) 产生 \(1\) 的贡献，但这里已经填好了，所以直接从 \(f_{i+1,i}\) 开始考虑即可，从 \(f_{i+1,i}\) 到 \(f_{n,m}\) 要对 \(n\) 产生 \(n-i-1\) 次贡献，从中选择 \(m-i\) 次对 \(m\) 产生贡献。

也就是 \(f_{i,i}\) 对 \(f_{n,m}\) 的贡献为 \(\dfrac{i\times k\times \text{C}_{n-i-1}^{m-i}}{2^{n-i}}\) 。

这个 \(2^{n-i}\) 显然，每次都是要 \(÷2\) 的，而 \(i\times k\) 表示 \(f_{i,i}\) 自身。

由此最后的答案就为：

\[\sum\limits_{i=1}^{m}\dfrac{i\times k\times \text{C}_{n-i-1}^{m-i}}{2^{n-i}}
\]

至于只循环到 \(m\) ，因为 \(Bob\) 只会选择 \(m\) 轮去加。

关于代码：首先需要预处理阶乘与每个 \(2^i\)，乘法逆元可用费马小定理 \(+\) 快速幂，因为预处理需要到 \(1e9\) 显然会炸。

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=1e6+10,P=1e9+7;
template<typename Tp> inline void read(Tp&x)
{
    x=0;register bool z=true;
    register char c=getchar();
    for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
    for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
    x=(z?x:~x+1);
}
int t,n,m,k,jc[N],inv2[N];
int qpow(int a,int b)
{
    int ans=1;
    for(;b;b>>=1)
    {
        if(b&1) (ans*=a)%=P;
        (a*=a)%=P;
    }
    return ans;
}
void pre()
{
    jc[0]=jc[1]=1;
    for(int i=2;i<=N-1;i++) jc[i]=(jc[i-1]*i)%P;
    inv2[0]=1,inv2[1]=2;
    for(int i=2;i<=N-1;i++) inv2[i]=(inv2[i-1]*2)%P;
}
int C(int m,int n)
{
    if(m==0||n==m) return 1;
    return (((jc[n]*qpow(jc[m],P-2))%P)*qpow(jc[n-m],P-2))%P;
}
signed main()
{
	#ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif
    pre();
    read(t);
    while(t--)
    {
        read(n),read(m),read(k);
        if(n==m)
        {
            cout<<(n*k)%P<<endl;
            continue;
        }
        int ans=0;
        for(int i=1;i<=m;i++)
            (ans+=(((((i*k)%P)*C(m-i,n-i-1))%P)*qpow(inv2[n-i],P-2))%P)%=P;
        cout<<ans<<endl;
    }
}

切切糕

• \(3.21\) 。

• 多倍经验。

这个乏味范围是小的，\(DP\) 即可。

贪心思想，\(Tinytree\) 会将优先权给尽可能大的糕，所以将 \(a_i\) 从大到小排序。

当其拥有优先权时，设 \(Kiana\) 会将 \(a_i\) 分成 \(x_i\) 与 \(a_i-x_i\) ，那么显然 \(Tinytree\) 会将 \(\min(x_i,a_i-x_i)\) 给 \(Kiana\) 。

定义 \(f_{i,j}\) 是 \(Kiana\) 在分完第 \(i\) 块，其中 \(Tinytree\) 用了 \(j\) 次优先权时分到的蛋糕大小。

与上面类似的，使 \(\min(f_{i,j-1}+x_i,f_{i,j}+a_i-x_i)\) 最大,有：

\[f_{i,j-1}+x_i=f_{i,j}+a_i-x_i=\dfrac{f_{i,j-1}+f_{i,j}+a_i}{2}
\]

最后答案为 \(sum-f_{n,m}\) ，\(sum\) 指 \(\sum\limits_{i=1}^na_i\) 。

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=2510;
const double eps=1e-12;
template<typename Tp> inline void read(Tp&x)
{
    x=0;register bool z=true;
    register char c=getchar();
    for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
    for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
    x=(z?x:~x+1);
}
int n,m;
double a[N],sum[N],f[N][N];
bool cmp(double a,double b) {return a-b>eps;}
signed main()
{
	#ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif
    read(n),read(m);
    for(int i=1;i<=n;i++) cin>>a[i];
    stable_sort(a+1,a+1+n,cmp);
    for(int i=1;i<=n;i++) sum[i]=sum[i-1]+a[i];
    for(int i=1;i<=n;i++)
        for(int j=0;j<=min(i,m);j++)
            if(j==0) f[i][j]=0;
            else if(i==j) f[i][j]=sum[i]/2.0;
            else f[i][j]=max((f[i-1][j-1]+f[i-1][j]+a[i])/2.0,f[i-1][j]);
    printf("%.6f",sum[n]-f[n][m]);
}

A - Helping People

• \(3.24\)

  主要是 \(3.21\) 打的，当时由于某些纸张问题没调出来，而中间经历了 \(whk\) 考试与放假，所以相隔了 \(3\) 天。

树形 \(DP\) ，概率 \(DP\) 。

首先我们需要明确他问的是啥：

• “好处”：所有人拥有的金额中的最大值。

• “期望”：从期望的本质去想 ，其意义为 \(\sum\limits_{i=1}^nq_ix_i\) ，也就是每个最大指乘上他的概率再加一起。

可见他问的是最大值的期望，并非期望的最大值。

我们发现他每个区间要么包含要么不相交，所以可以将其转化为一个树的结构去跑树形 \(DP\) ，类似于线段树的一个结构，每个节点表示一个区间。

当然他可能是个森林，所以再加一个 \([1,n]\) 的区间，对应概率为 \(0\) 的节点作为根节点。

那么我们将他按照区间长度从大到小排序，就可以简单的简称一棵树。

定义 \(a_i\) 为第 \(i\) 个人的初始值，对于区间 \(i\) 中 \(a\) 的最大值 为 \(mx_i\) 。不难发现这个区间最后的最大值 \(\in {mx_i\sim mx_i+m}\) 。

那么我们定义 \(f_{i,j}\) 为对于区间 \(i\) 的最大值 \(\leq mx_i+j\) 时的概率，对此有转移方程：

\[f_{i,j}=q_i\times f_{son_i,j-mx_{son_i}+mx_i-1}+(1-q_i)\times f_{son_i,j-mx_{son_i}+mx_i}
\]

最后答案为 \(\sum\limits_{i=0}^m(f_{1,i}-f_{1,i-1})\times (i+mx_1)\) ，因为显然第 \(1\) 个区间为 \([1,n]\) 。当然 \(0\) 要特判。

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=1e5+10,M=5010;
template<typename Tp> inline void read(Tp&x)
{
    x=0;register bool z=true;
    register char c=getchar();
    for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
    for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
    x=(z?x:~x+1);
}
int n,m,mx[N][20];
double ans,f[M][M];
vector<int>son[N];
struct aa
{
    int l,r,mx;
    double p;
}e[M];
bool cmp(aa a,aa b) {return a.r-a.l>b.r-b.l;}
void init()
{
    for(int j=1;j<=log2(n);j++)
        for(int i=1;i<=n-(1<<j)+1;i++)
            mx[i][j]=max(mx[i][j-1],mx[i+(1<<(j-1))][j-1]);
}
int ask(int l,int r)
{
    int t=log2(r-l+1);
    return max(mx[l][t],mx[r-(1<<t)+1][t]);
}
void build()
{
    stable_sort(e+1,e+1+m,cmp);
    for(int i=1;i<=m;i++)
        for(int j=i-1;j>=1;j--)
            if(e[j].l<=e[i].l&&e[j].r>=e[i].r)
            {
                son[j].push_back(i);
                break;
            }
}
void dfs(int i)
{
    f[i][0]=1-e[i].p;
    for(int j:son[i])
        dfs(j),
        f[i][0]*=f[j][min(m,e[i].mx-e[j].mx)];
    for(int k=1;k<=m;k++)
    {
        double sum1=1,sum2=1;
        for(int j:son[i])
            sum1*=f[j][min(m,k-e[j].mx+e[i].mx-1)],
            sum2*=f[j][min(m,k-e[j].mx+e[i].mx)];
        f[i][k]=e[i].p*sum1+(1-e[i].p)*sum2;
    }
}
signed main()
{
	#ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif
    read(n),read(m);
    for(int i=1;i<=n;i++)
        read(mx[i][0]);
    init();
    for(int i=1;i<=m;i++)
        read(e[i].l),read(e[i].r),
        cin>>e[i].p,
        e[i].mx=ask(e[i].l,e[i].r);
    e[++m].l=1,e[m].r=n,e[m].p=0,e[m].mx=ask(1,n);
    build();
    dfs(1);
    for(int i=0;i<=m;i++)
        ans+=(f[1][i]-(i==0?0:f[1][i-1]))*(i+e[1].mx);
    printf("%.9f",ans);
}

C - Positions in Permutations

• \(3.26\)

\(DP+\) 容斥 \(+\) 组合计数

定义 \(f_{i,j,k,l}\) 为前 \(i\) 个数中有 \(j\) 个是好的，第 \(i\) 位和第 \(i+1\) 位被占用情况分别为 \(l,k\) （布尔）。

去思考转移方程，有：

\[f_{i,j,0,0}=f_{i-1,j,0,0}+f_{i-1,j,1,0}+f_{i-1,j-1,0,0}
\]

\[f_{i,j,1,0}=f_{i-1,j,0,1}+f_{i-1,j,1,1}+f_{i-1,j-1,0,1}
\]

\[f_{i,j,0,1}=f_{i-1,j-1,0,0}+f_{i-1,j-1,1,0}
\]

\[f_{i,j,1,1}=f_{i-1,j-1,0,1}+f_{i-1,j-1,1,1}
\]

按照 \(i-1,i,i+1\) 是否被选分别考虑即可，其中后两个因为选了 \(i+1\) 所以一定多了一个“好的”，就只有 \(j-1\) 的情况。

那么所有排列中至少有 \(i\) 个是“好的”的方案数就是 \(ans_i=(f_{n,i,1,0}+f_{n,i,0,0})\times (n-i)!\)

于是发现需要容斥。

思考 \(f_{n,i}\) 的贡献为 \(\text{C}_i^m\times ans_i\) （\(m\leq i\leq n\)），于是通过容斥，有：

\[\sum\limits_{i=m}^n\times (-1)^{i-m}\times \text{C}_{i}^m\times ans_i
\]

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=1010,P=1e9+7;
template<typename Tp> inline void read(Tp&x)
{
    x=0;register bool z=true;
    register char c=getchar();
    for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
    for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
    x=(z?x:~x+1);
}
int n,m,f[N][N][2][2],jc[N],anss,ans[N],C[N];
int qpow(int a,int b)
{
    int ans=1;
    for(;b;b>>=1)
    {
        if(b&1) (ans*=a)%=P;
        (a*=a)%=P;
    }
    return ans;
}
void pre()
{
    jc[0]=jc[1]=1;
    for(int i=2;i<=N-1;i++)
        jc[i]=(jc[i-1]*i)%P;
    C[m]=1;
    for(int i=m+1;i<=n;i++)
        C[i]=(((C[i-1]*i)%P)*qpow(i-m,P-2))%P;
}
signed main()
{
	#ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif
    read(n),read(m);
    pre();
    f[1][1][0][1]=f[1][0][0][0]=1;
    for(int i=2;i<=n;i++)
        for(int j=0;j<=i;j++)
        {
            (f[i][j][0][0]+=f[i-1][j][1][0]+f[i-1][j][0][0])%=P;
            if(j) (f[i][j][0][0]+=f[i-1][j-1][0][0])%=P;
            (f[i][j][1][0]+=f[i-1][j][0][1]+f[i-1][j][1][1])%=P;
            if(j) (f[i][j][1][0]+=f[i-1][j-1][0][1])%=P;
            if(i!=n&&j)
                (f[i][j][0][1]+=f[i-1][j-1][0][0]+f[i-1][j-1][1][0])%=P,
                (f[i][j][1][1]+=f[i-1][j-1][0][1]+f[i-1][j-1][1][1])%=P;
        }
    for(int i=m;i<=n;i++)
        ans[i]=(((f[n][i][1][0]+f[n][i][0][0])%P)*jc[n-i])%P;
    for(int i=m,t=0;i<=n;i++,t++)
        (anss+=(((qpow(-1,t)*C[i])%P)*ans[i])%P+P)%=P;
    cout<<anss;
}

F - ZS Shuffles Cards

• \(3.30\)

  前几天去调模拟赛和分块了。

  感觉挺水的，为啥评 \(3000\) ，\(luogu\) 上都降紫了，个人感觉比 \(A\) 简单多了。

概率期望 \(DP\) 。

首先如果直接跑期望 \(DP\) 的话。

\(f_i\) 表示已经取了 \(i\) 张数字牌，还需要的期望，\(f_n=0\) 。

• \(\dfrac{n-i}{n+m-i}\) 的概率取到新的牌。

• \(\dfrac{m}{n+m-i}\) 的概率取到 joker ，此时就要从头开始了。

那么有:

\[f_i=\dfrac{n-i}{n+m-i}\times f_{i+1}+\dfrac{m}{n+m-i}\times f_0+1
\]

显然这个式子非常好想，但是发现不满足无后效性，不能递推实现，需要高斯消元，那么 \(O(n^3)\) 显然 \(TLE\) 了，而且及其难打。

所以需要转变思路。

不放将期望分成两个部分：

• 轮数的期望。

• 每轮所需秒数的期望。

那么显然这两个东西乘起来就是最后的答案。

• 先求轮数的期望：

  定义 \(f_i\) 表示还需要取 \(i\) 张数字牌，换而言之就是已经取了 \(n-i\) 张数字牌时还需要的轮数的期望。

  有 \(f_0=1\) ，因为当所有数字牌都取完时，根据题意，还需要再取到一张 joker 才能结束，剩下的牌显然都是 joker 了，所以还需要 \(1\) 轮。

  发现是正着跑的，并非通常的倒着跑，其实没有太大的区别，只是这么写的话代码能少打几个字，仔细想的话，已经取了 \(i\) 张数字牌和还需要 \(i\) 张数字牌没有本质的区别。

  那么转移方程也非常好想：

  \[f_i=\dfrac{i}{m+i}\times f_{i-1}+\dfrac{m}{m+i}\times (f_i+1)
  \]

  化简为：

  \[f_i=f_{i-1}+\dfrac{m}{i}
  \]

  解释一下：

  • \(\dfrac{i}{m+i}\) 的概率取到新的牌。

  • \(\dfrac{m}{m+i}\) 的概率取到 joker ，显然就需要开启新的一轮了。

• 每轮所需秒数的期望：

  • 第一种理解方法：

    我们发现取到的是哪一个数字牌不重要，重要的是取到的是数字牌。

    那么不放将这一堆数字牌看做一个，那么在取到 joker 前一个取到数字牌的概率就为 \(\dfrac{1}{m+1}\) 。

    不难发现该式子表示的就是对于每一个数字牌，在他后面开启新的一轮的概率。

    思考期望的定义：\(\sum\limits_{i=1}^nq_i\times x_i\) ，每一张牌他对秒数的贡献都为 \(1\) ，而在他后面开启新的一轮的概率为 \(\dfrac{1}{m+1}\) 。

    那么有每轮的秒数期望值 \(=1+\sum\limits_{i=1}^n 1 \times \dfrac{1}{m+1}=1+\dfrac{n}{m+1}\) ，至于为什么 \(+1\) ，取到 joker 也算一秒。

  • 第二种理解方法：

    我们知道如果对于这一秒他开启新的一局的概率为 \(\dfrac{1}{a}\) ，那么他这一局进行的秒数的期望就为 \(a\) 。

    那么对于这个场景，我们设他在第 \(i\) 秒结束，在第 \(i\) 秒时他取到 joker 的概率为 \(\dfrac{m}{n+m-(i-1)}\) ，那么取他的倒数，有：

    \[i=\dfrac{n+m-(i-1)}{m}
    \]

    解这个方程，有 \(i=\dfrac{n+m+1}{m+1}=1+\dfrac{n}{m+1}\) 。

最后答案就为 \(f_n\times (1+\dfrac{n}{m+1})\) 。

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define endl '\n'
#define sort stable_sort
using namespace std;
const int N=4e6+10,P=998244353;
template<typename Tp> inline void read(Tp&x)
{
    x=0;register bool z=true;
    register char c=getchar();
    for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
    for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
    x=(z?x:~x+1);
}
void wt(int x){if(x>9)wt(x/10);putchar((x%10)+'0');}
void write(int x){if(x<0)putchar('-'),x=~x+1;wt(x);}
int n,m,f[N];
int qpow(int a,int b)
{
    int ans=1;
    for(;b;b>>=1)
    {
        if(b&1) (ans*=a)%=P;
        (a*=a)%=P;
    }
    return ans;
}
signed main()
{
	#ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif
    read(n),read(m);
    f[0]=1;
    for(int i=1;i<=n;i++)
        f[i]=(f[i-1]+(m*qpow(i,P-2))%P)%P;
    cout<<(f[n]*(1+(n*qpow(m+1,P-2))%P)%P)%P;
}

H - Tavas in Kansas

• \(4.1\)

  周测没和喵喵请下来假。

分别以 \(s,t\) 为起点先跑两边 \(dijkstra\) ，处理出其到每个点的距离 \(d_{s,i},d_{t,i}\) 。

那么根据此我们可以知道每个点他距离 \(s,t\) 分别是第几远的，并将其离散化成 \(x_i,y_i\) ，由此形成一个 \(n\times n\) 矩阵。

Tavas每次取一行，Nafas每次取一列，那么现在问题就转化的不那么复杂了。

我们想要知道 Tavas 和 Nafas 谁的得分高，并不需要知道其各自的具体分数，所以定义 \(f_{i,j,0/1}\) 分别表示目前 Tavas 取到第 \(i\) 行，Nafas 取到第 \(j\) 列时，Tavas 与 Nafas 的得分差，其中 \(0\) 表示轮到 Tavas 取，\(1\) 表示轮到 Nafas 取。

于是在此遇到三个问题：

• 最后答案是轮到谁的问题。

• 取过的点不能再取的问题。

• 每次必须取一个新点的问题。

一次解决这些问题：

• 最后答案轮到谁？

  发现从前往后递推，到答案时我们需要处理出轮到谁。

  然而我们知道 Tavas 为先手，如果从后往前跑的话，本质上不会影响答案，且知道到答案时一定是轮到 Tavas ，所以我们选择从后往前递推。

• 取过的点不能再取。

  我们现在已知他取到第 \(i\) 行第 \(j\) 列，也就是说在第 \(i\) 行第 \(j\) 列之前都已经取过了。

  • 那么对于 Tavas ，他可以取 \(i,j\) 到 \(i,n\) 中的点。

  • 同样对于 Nafas ，她可以取 \(i,j\) 到 \(n,j\) 中的点。

  问题解决。

• 每次都要取到新点。

  根据我们上一个问题的分析，我们知道两人本次活动取什么范围内的点。

  首先该范围内的点一定是没有取过的。

  那么如果该范围存在点，接等同于存在新点，于是可以转移。

  不妨用一个新的变量处理每个范围内有几个点。

上面所说的一些均可以用二维前缀和维护。

转移方程：

\[f_{i,j,0}=\begin{cases} f_{i+1,j,0} & sum2(i,j,i,n)=0 \\ \max(f_{i+1,j,0},f_{i+1,j,1})+sum1(i,j,i,n) & sum2(i,j,i,n) \ne 0 \end{cases}
\]

\[f_{i,j,1}=\begin{cases} f_{i,j+1,0} & sum2(i,j,n,j)=0 \\ \min(f_{i,j+1,0},f_{i,j+1,1})-sum1(i,j,n,j) & sum2(i,j,n,j) \ne 0 \end{cases}
\]

因为我们 \(f\) 表示的是 Tavas 得分与 Nafas 得分的差，所以 Tavas 希望差尽可能大，Nafas 希望得分尽可能小。

其中 \(sum1(x1,y1,x2,y2)\) 表示从 \(x1,y1\) 到 \(x2,y2\) 这一范围内权值和，\(sum2(x1,y1,x2,y2)\) 表示 \(x1,y1\) 到 \(x2,y2\) 这一范围点的个数。

最后根据 \(f_{1,1,0}\) 的正负输出答案即可。

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define endl '\n'
#define sort stable_sort
using namespace std;
const int N=2010,M=2e5+10;
template<typename Tp> inline void read(Tp&x)
{
    x=0;register bool z=true;
    register char c=getchar();
    for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
    for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
    x=(z?x:~x+1);
}
int n,m,s,t,p[N],x[N],y[N],d[N],dis[N],a[N][N],b[N][N],sum1[N][N],sum2[N][N],f[N][N][2];
bool v[N];
int head[N],to[M],w[M],nxt[M],tot;
void add(int x,int y,int z)
{
    nxt[++tot]=head[x];
    to[tot]=y;
    w[tot]=z;
    head[x]=tot;
}
void dijkstra(int s,int a[])
{
    memset(d,0x3f,sizeof(d));
    memset(v,0,sizeof(v));
    priority_queue<pair<int,int>>q;
    d[s]=0;
    q.push(make_pair(0,s));
    while(!q.empty())
    {
        int u=q.top().second;
        q.pop();
        if(!v[u])
        {
            v[u]=1;
            for(int i=head[u];i;i=nxt[i])
            {
                int v=to[i],z=w[i];
                if(d[v]>d[u]+z)
                    d[v]=d[u]+z,
                    q.push(make_pair(-d[v],v));
            }
        }
    }
    for(int i=1;i<=n;i++)
        dis[i]=d[i];
    sort(dis+1,dis+1+n);
    dis[0]=unique(dis+1,dis+1+n)-(dis+1);
    for(int i=1;i<=n;i++)
        a[i]=lower_bound(dis+1,dis+1+dis[0],d[i])-dis;
}
int ask(int x,int y,int xx,int yy,int sum[N][N])
{
    return sum[xx][yy]-sum[x-1][yy]-sum[xx][y-1]+sum[x-1][y-1];
}
signed main()
{
	#ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif
    read(n),read(m),read(s),read(t);
    for(int i=1;i<=n;i++) read(p[i]);
    for(int i=1,u,v,z;i<=m;i++)
        read(u),read(v),read(z),
        add(u,v,z),
        add(v,u,z);
    dijkstra(s,x),dijkstra(t,y);
    for(int i=1;i<=n;i++)
        a[x[i]][y[i]]+=p[i],
        b[x[i]][y[i]]++;
    for(int i=1;i<=n+1;i++)
        for(int j=1;j<=n+1;j++)
            sum1[i][j]=sum1[i-1][j]+sum1[i][j-1]-sum1[i-1][j-1]+a[i][j],
            sum2[i][j]=sum2[i-1][j]+sum2[i][j-1]-sum2[i-1][j-1]+b[i][j];
    for(int i=n+1;i>=1;i--)
        for(int j=n+1;j>=1;j--)
            if(i!=n+1||j!=n+1)
                f[i][j][0]=(ask(i,j,i,n,sum2)==0)?f[i+1][j][0]:max(f[i+1][j][0],f[i+1][j][1])+ask(i,j,i,n,sum1),
                f[i][j][1]=(ask(i,j,n,j,sum2)==0)?f[i][j+1][1]:min(f[i][j+1][0],f[i][j+1][1])-ask(i,j,n,j,sum1);
    if(f[1][1][0]<0) puts("Cry");
    if(f[1][1][0]==0) puts("Flowers");
    if(f[1][1][0]>0) puts("Break a heart");
}

E - Bear and Cavalry

• \(4.1\)

  关于大多数人都只做了五六道时就把所有题都讲了这件事。

  不出意外明天就要开字符串了。

结论题。

首先如果不考虑限制的话，将 \(w_i,h_i\) 都从小到大排序，显然有答案为 \(\sum\limits_{i=1}^nw_ih_i\) 。

接下来考虑不能骑自己马怎么搞。

结论：满足限制的匹配单元仅有以下 \(4\) 种：

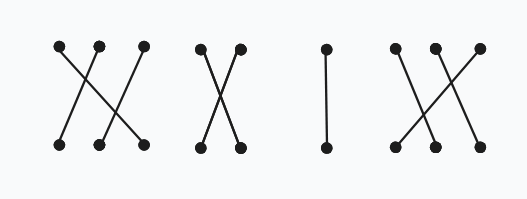
先从 \(n=3\) 开始分析：

定义 \(ban_i\) 表示 \(i\) 的马。

• \(ban_1\neq 1,ban_2\neq 2,ban3\neq 3。\)

  

• \(ban_1\neq 1,ban_2=2,ban_3=3。\)

  

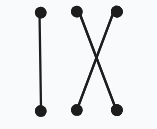
• \(ban_1=1,ban_2=2,ban_3=3。\)

  
  
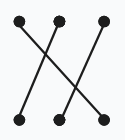
  或
  
  

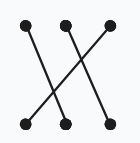
以此类以的分析，当 \(n>3\) 时，也只会产生上述 \(4\) 种匹配单元。

那么对于每次修改，至多对左右两边三个产生影响，有：

\[f_{i}=\max \begin{cases} f_{i-1}+w_{i}h_{i} \\ f_{i-2}+w_{i}h_{i-1}+w_{i-1}h_{i} \\ f_{i-3}+\max(w_{i}h_{i-1}+w_{i-1}h_{i-2}+w_{i-2}h_{i},w_{i}h_{i-2}+w_{i-1}h_{i}+w_{i-2}h_{i-1}) \end{cases}
\]

如果暴力修改的话，发现会 \(TLE\) ，但是只 \(TLE\) 一点点，发现时限是 \(3000ms\) ，我们不卡常都对不起这个 \(3000ms\) 。

发现因为在转移时用了多个 \(if\) ，不放在每次转移前先将其 \(w_ih_i\) （以此类推）处理出来，能少好多 \(if\) 。

于是我们就能勉强通过此题，\(3000ms\) 的时限用了 \(2700ms\) ，甚至因为评测姬波动有时候还会 \(TLE\) ，不过没关系，多交几遍就 \(AC\) 了。

显然我们是卡常过的，并非正解。

所以负责任的将正解的题解放在这里：\(@wang54321\)的题解 。

懒得打正解了。

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define endl '\n'
#define sort stable_sort
using namespace std;
const int N=3e5+10;
template<typename Tp> inline void read(Tp&x)
{
    x=0;register bool z=true;
    register char c=getchar();
    for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
    for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
    x=(z?x:~x+1);
}
int n,m,posa[N],posb[N],ban[N],w[N][4],f[N];
struct aa
{
    int w,id;
}a[N],b[N];
bool cmp(aa a,aa b) {return a.w<b.w;}
signed main()
{
	#ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif
    read(n),read(m);
    for(int i=1;i<=n;i++)
        read(a[i].w),
        a[i].id=i;
    for(int i=1;i<=n;i++)
        read(b[i].w),
        b[i].id=i;
    sort(a+1,a+1+n,cmp),sort(b+1,b+1+n,cmp);
    for(int i=1;i<=n;i++)
        posa[a[i].id]=posb[b[i].id]=i;
    for(int i=1;i<=n;i++)
        ban[i]=posb[a[i].id];
    for(int i=1;i<=n;i++)
    {
        w[i][1]=-0x3f3f3f3f;
        if(i-1>=0&&ban[i]!=i)
            w[i][1]=max(w[i][1],a[i].w*b[i].w);
        if(i-2>=0&&ban[i]!=i-1&&ban[i-1]!=i)
            w[i][2]=max(w[i][2],a[i].w*b[i-1].w+a[i-1].w*b[i].w);
        if(i-3>=0&&ban[i]!=i-2&&ban[i-1]!=i&&ban[i-2]!=i-1)
            w[i][3]=max(w[i][3],a[i].w*b[i-2].w+a[i-1].w*b[i].w+a[i-2].w*b[i-1].w);
        if(i-3>=0&&ban[i]!=i-1&&ban[i-1]!=i-2&&ban[i-2]!=i)
            w[i][3]=max(w[i][3],a[i].w*b[i-1].w+a[i-1].w*b[i-2].w+a[i-2].w*b[i].w);
    }
    for(int x,y,l,r;m;m--)
    {
        read(x),read(y);
        swap(ban[posa[x]],ban[posa[y]]);
        l=max(1ll,posa[x]-3),r=min(n,posa[x]+3);
        for(int i=l;i<=r;i++)
        {
            w[i][1]=w[i][2]=w[i][3]=-0x3f3f3f3f;
            if(i-1>=0&&ban[i]!=i)
                w[i][1]=max(w[i][1],a[i].w*b[i].w);
            if(i-2>=0&&ban[i]!=i-1&&ban[i-1]!=i)
                w[i][2]=max(w[i][2],a[i].w*b[i-1].w+a[i-1].w*b[i].w);
            if(i-3>=0&&ban[i]!=i-2&&ban[i-1]!=i&&ban[i-2]!=i-1)
                w[i][3]=max(w[i][3],a[i].w*b[i-2].w+a[i-1].w*b[i].w+a[i-2].w*b[i-1].w);
            if(i-3>=0&&ban[i]!=i-1&&ban[i-1]!=i-2&&ban[i-2]!=i)
                w[i][3]=max(w[i][3],a[i].w*b[i-1].w+a[i-1].w*b[i-2].w+a[i-2].w*b[i].w);
        }
        l=max(1ll,posa[y]-3),r=min(n,posa[y]+3);
        for(int i=l;i<=r;i++)
        {
            w[i][1]=w[i][2]=w[i][3]=-0x3f3f3f3f;
            if(i-1>=0&&ban[i]!=i)
                w[i][1]=max(w[i][1],a[i].w*b[i].w);
            if(i-2>=0&&ban[i]!=i-1&&ban[i-1]!=i)
                w[i][2]=max(w[i][2],a[i].w*b[i-1].w+a[i-1].w*b[i].w);
            if(i-3>=0&&ban[i]!=i-2&&ban[i-1]!=i&&ban[i-2]!=i-1)
                w[i][3]=max(w[i][3],a[i].w*b[i-2].w+a[i-1].w*b[i].w+a[i-2].w*b[i-1].w);
            if(i-3>=0&&ban[i]!=i-1&&ban[i-1]!=i-2&&ban[i-2]!=i)
                w[i][3]=max(w[i][3],a[i].w*b[i-1].w+a[i-1].w*b[i-2].w+a[i-2].w*b[i].w);
        }
        f[0]=0;
        for(int i=1;i<=n;i++)
        {
            if(i-1>=0)
                f[i]=f[i-1]+w[i][1];
            if(i-2>=0)
                f[i]=max(f[i],f[i-2]+w[i][2]);
            if(i-3>=0)
                f[i]=max(f[i],f[i-3]+w[i][3]);
        }
        cout<<f[n]<<endl;
    }
}

总结

动态规划专题到这儿就结束了，虽然还有 \(D,G\) 两道题设计未学过知识点的题没有做，实际上这个专题最早开还是有原因的，毕竟这东西涉及未学过知识点最少，且主要是锻炼思维，之前应该是从来没有做过这样难度的 \(DP\) ，同时尽可能的锻炼独立思考能力，能不 \(hè\) 坚决不 \(hè\) ，在这里入门晚、过知识点太仓促的缺陷也体现出来了，需要在今后的学习中努力弥补。