POJ3684 Physics Experiment 【物理】

Physics Experiment

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 1031		Accepted: 365		Special Judge

Description

Simon is doing a physics experiment with N identical balls with the same radius of R centimeters. Before the experiment, all N balls are fastened within a vertical tube one by one and the lowest point of the lowest ball is H meters
above the ground. At beginning of the experiment, (at second 0), the first ball is released and falls down due to the gravity. After that, the balls are released one by one in every second until all balls have been released. When a ball hits the ground, it
will bounce back with the same speed as it hits the ground. When two balls hit each other, they with exchange their velocities (both speed and direction).

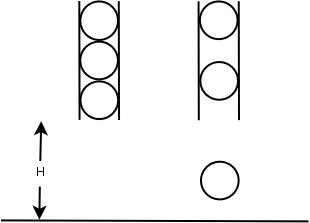
Simon wants to know where are the N balls after T seconds. Can you help him?

In this problem, you can assume that the gravity is constant: g = 10 m/s².

Input

The first line of the input contains one integer C (C ≤ 20) indicating the number of test cases. Each of the following lines contains four integers N, H, R, T.

1≤ N ≤ 100.

1≤ H ≤ 10000

1≤ R ≤ 100

1≤ T ≤ 10000

Output

For each test case, your program should output N real numbers indicating the height in meters of the lowest point of each ball separated by a single space in a single line. Each number should be rounded to 2 digit after the decimal point.

Sample Input

2
1 10 10 100
2 10 10 100

Sample Output

4.95
4.95 10.20

Source

POJ Founder Monthly Contest – 2008.08.31, Simon

/*
** Problem: POJ3684
** Status: Accepted
** Running Time: 0ms
** Author: Changmu
**
** 题意：算是我的第一道物理题吧，题意是N个球叠放在一起，每隔一秒最下边的球
** 就掉落下来，给定最以下球的底的高度，求T秒后每一个球的底的离地高度，g=10m/s^2.
**
** 题解：因为碰撞时两个球的速度交换了。实际上能够看做两个球互相穿越了彼此。但
** 又因为球的顺序不会变。所以求得的结果排序后就是答案。
*/
 
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <algorithm>
 
#define maxn 105
const double g = 10.0;
 
int N, H, R, T;
double Y[maxn];
 
double cal(int k) {
    if(k < 0) return H;
    double t = (double)sqrt(2.0 * H / g);
    int m = (int)(k / t);
    if(m & 1) {
        double t1 = (m + 1) * t - k;
        return H - g * t1 * t1 / 2;
    } else {
        double t1 = k - m * t;
        return H - g * t1 * t1 / 2;
    }
}
 
int main() {
    int t, i;
    scanf("%d", &t);
    while(t--) {
        scanf("%d%d%d%d", &N, &H, &R, &T);
        for(i = 0; i < N; ++i)
            Y[i] = cal(T - i);
        std::sort(Y, Y + N);
        for(i = 0; i < N; ++i)
            printf("%.2lf%c", Y[i] + 2.0*R*i/100.0, i==N-1?'\n':' ');
    }
    return 0;
}